Outstanding Info About What Is Smoothing In Math Gnuplot Smooth Lines

For instance, if your surface is.

What is smoothing in math. The controlling input of the exponential smoothing calculation is defined as the smoothing factor or the smoothing constant. Graph smoothing, also known as smoothing away or smoothing out, is the process of replacing edges e^'=v_iv_j and e^ ('')=v_jv_k incident at a vertex v_j of vertex degree 2 by a single new edge e=v_iv_k and removing. The number of continuous derivatives necessary for a function to be considered smooth depends on the problem at hand, and may vary from.

A smooth function can be discontinuous. Smooth point of a function). According to wikipedia, a smooth function is a function that has derivatives of all orders.

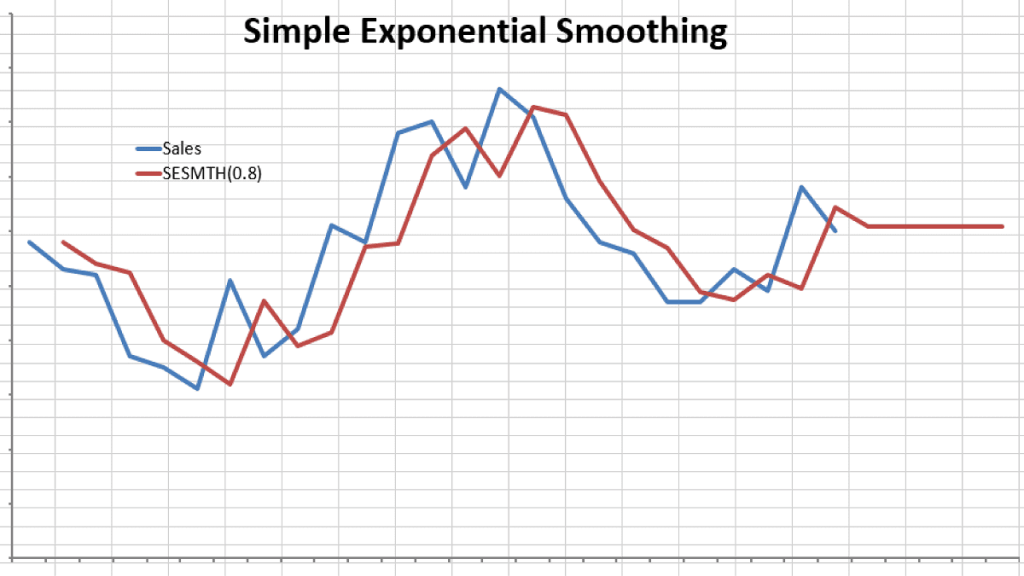
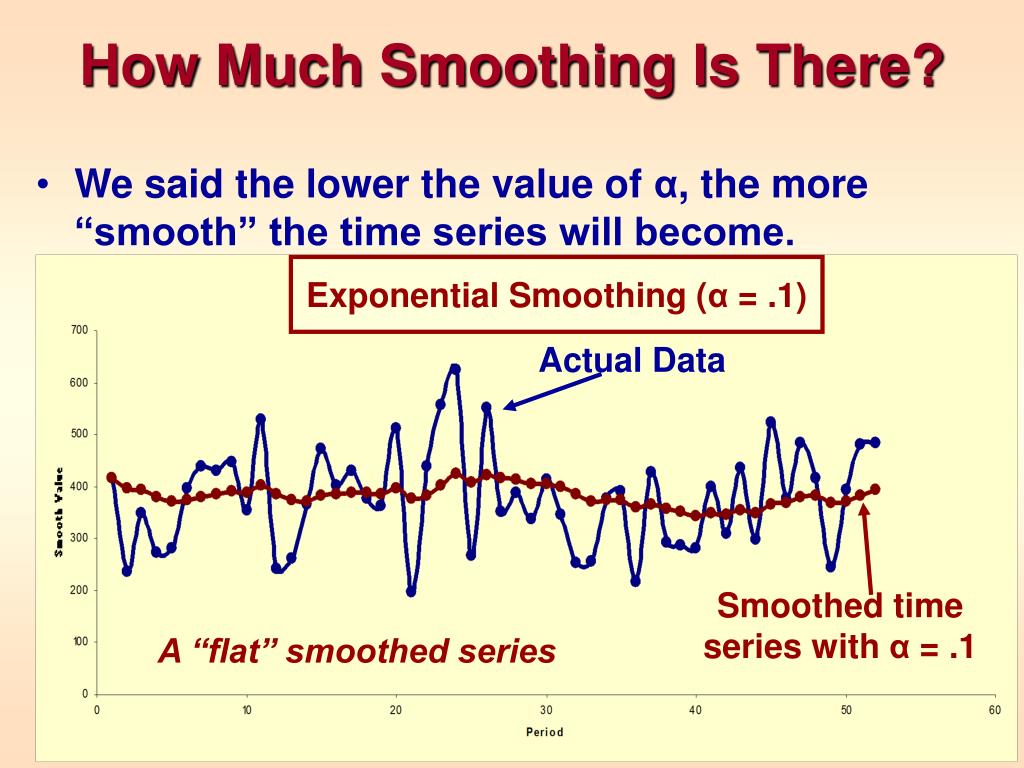
Exponential smoothing is a broadly accurate principle for smoothing time series data using the exponential window function. It is called exponential moving average, below is a code explanation how it is created. It is one of the main problems defined by norbert wiener.

I don't understand what this means if the case was for example the function. It is designed to detect trends in the presence of noisy data in cases in which the shape of the trend is unknown. Korablev y (2022) restoration of the product consumption rate with integral cubic smoothing spline, study of the best smoothing parameter choice acta applicandae mathematicae:

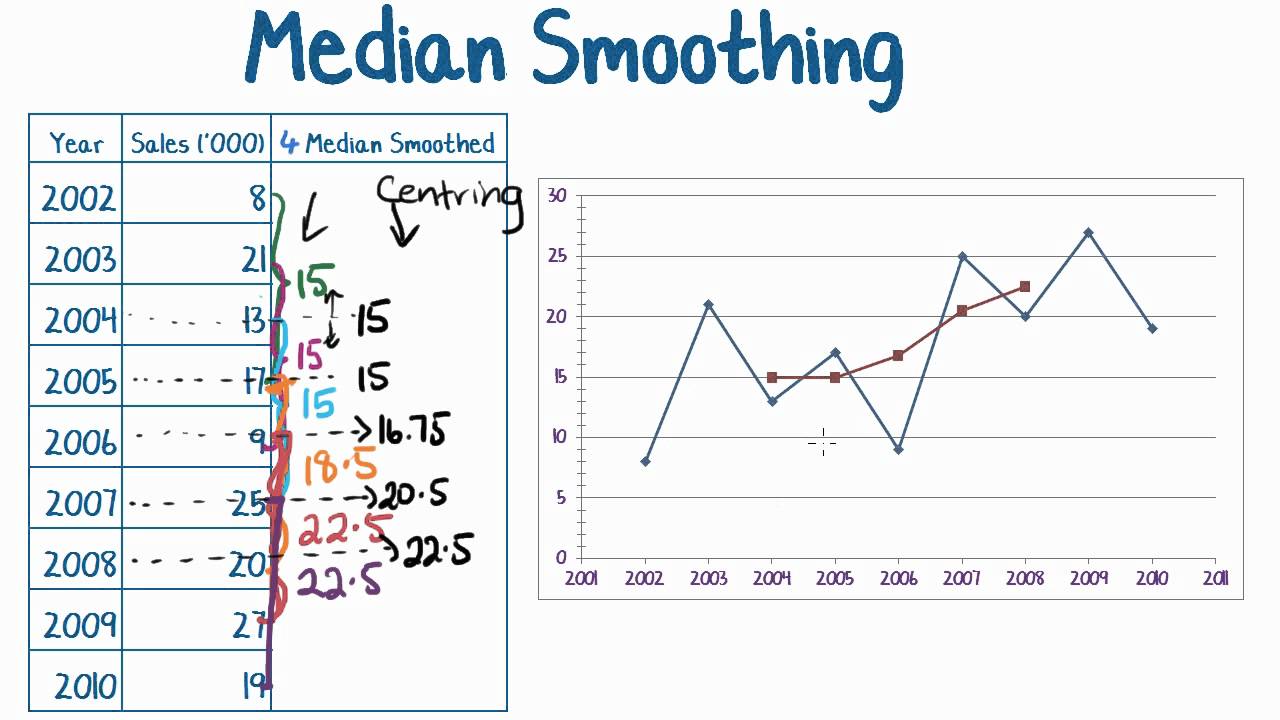
A function can therefore be said to be smooth over a restricted interval such as (a,b) or [a,b]. The smoothing problem (not to be confused with smoothing in statistics, image processing and other contexts) is the problem of estimating an unknown probability density function recursively over time using incremental incoming measurements. Smoothing methods often have an associated tuning parameter which is used to control the extent of smoothing.

This makes the image seem to pop out the screen and give it a more ‘detailed look’ but look closer and this isn’t the case. In other words, the older the data, the less priority (“weight”) the data is given; F(x) = 1 + 2x f ( x) = 1 + 2 x.

What is exponential smoothing? Exponential smoothing of time series data assigns exponentially decreasing weights for newest to oldest observations. In applications, when you say the curve is smooth it means till the derivatives you are interested in the curve has to be continuous.

Smoothness is a relative concept and is problem specific. Newer data is seen as more relevant and is assigned more weight. The thing is that smoothness is a property of linear approximation :

In mathematical analysis, the smoothness of a function is a property measured by the number, called differentiability class, of continuous derivatives it has over its domain. This can be differentiated only twice. In other words, they are continuous, differentiable, and so on for each derivative.

A smooth function is a function that has continuous derivatives up to some desired order over some domain. [1] a function of class is a function of smoothness at least k; A smoothing operator a ∈ c∞(x;e,f) is of finite rank if and only if there are elements f i ∈ c ∞ (x;f), e i ∈ c ∞ (x;e ′ ) i = 1,.,n and ν ∈ c ∞ (x;ω) such that