Heartwarming Info About What Is A Continuous Graph Dotted Line

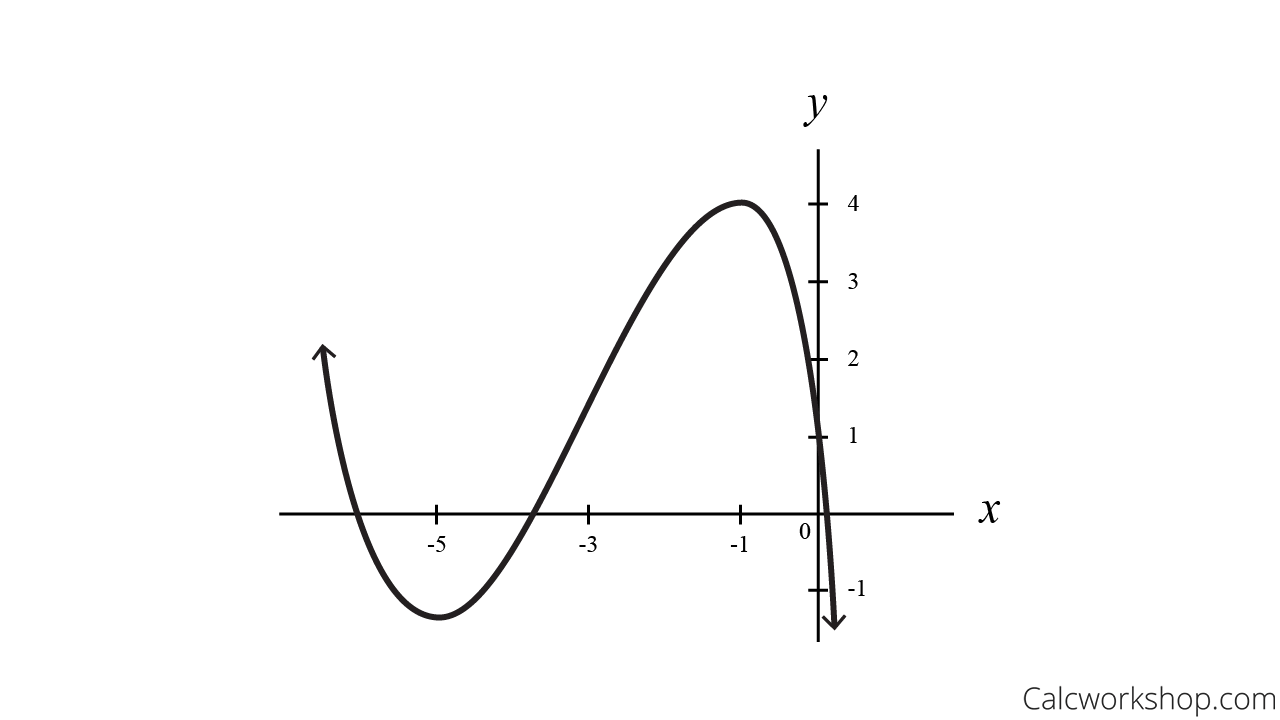
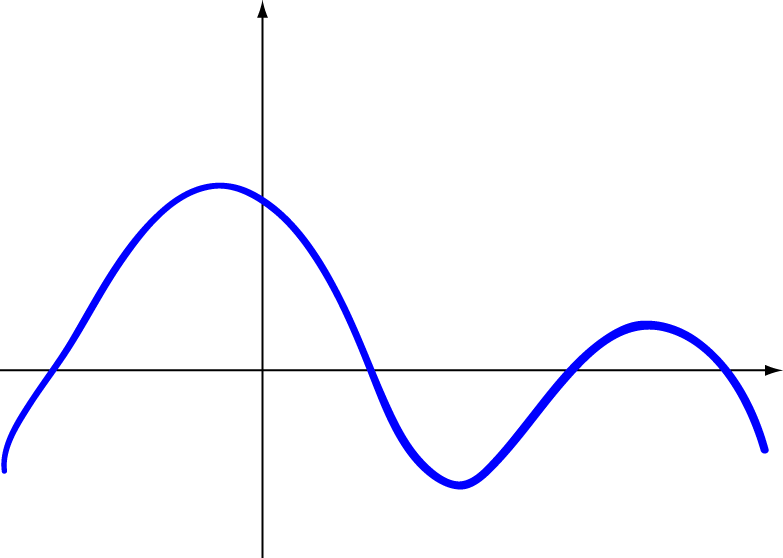
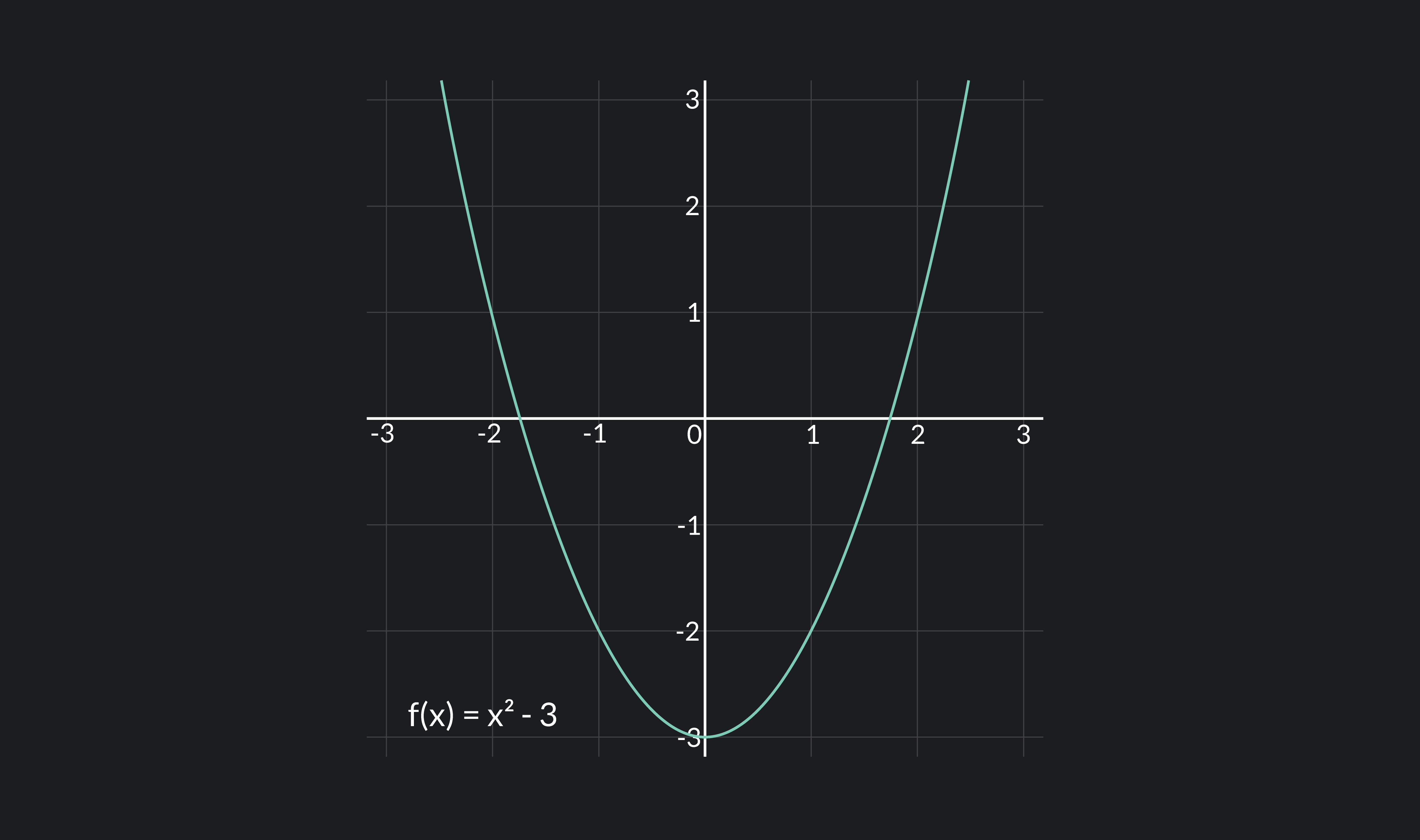
A function is continuous if its graph has no breaks or holes.

What is a continuous graph. The graph in the last example has only two discontinuities since there are only two places where we would have to. This capability is crucial for ensuring the trustworthy use and deployment of mode Many functions have the property that their graphs can be traced with a pencil without lifting the pencil from the page.

For help with continuous and discrete functions on your calculator, click here! Otherwise, the function is not continuous over that interval. That is not a formal definition, but it helps you understand the idea.

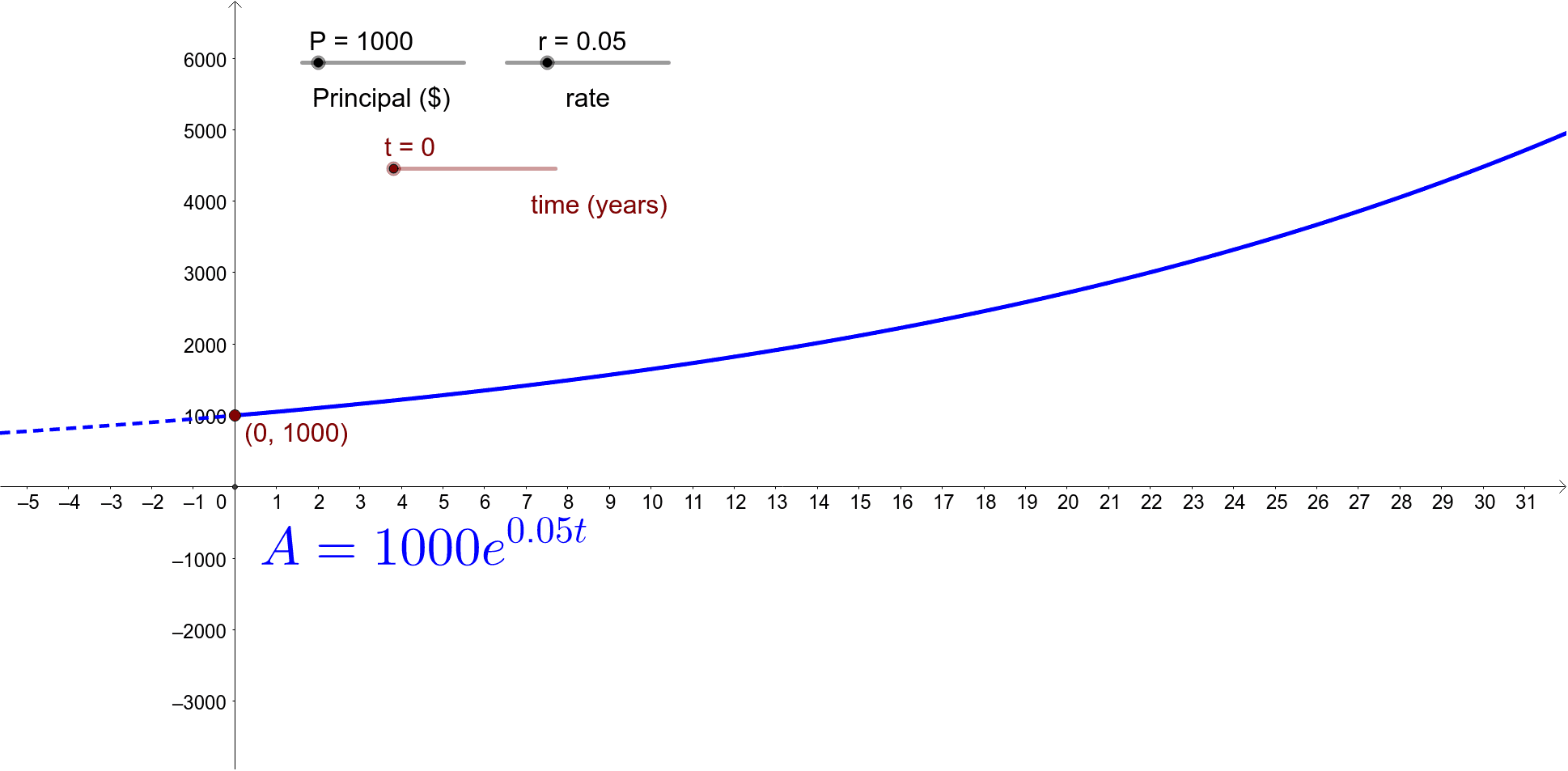
The graph continues to the right to extremely large speeds, but to the left the graph must end at zero (since a molecule can't have a speed less than zero). A continuous graph is a linear graph that describes the continuity of numbers along the x horizontal axis. Let's take a look at a comparison of these concepts:

A function can be continuous at a point, but not be differentiable there. How to determine if a function is continuous on a graph. Many functions have discontinuities (i.e.

Their graphs won’t contain any asymptotes or signs of discontinuities as well. We begin our investigation of continuity by exploring what it means for a function to have continuity at a point. Continuous functions are functions that have no restrictions throughout their domain or a given interval.

That you could draw without lifting your pen from the paper. Of the five graphs below, which shows a function that is continuous at x = a x = a? Continuous and discrete graphs visually represent functions and series, respectively.

In other words, if the line is continuous, the graph is continuous. Additionally, we demonstrate that the coherent. Intuitively, a function is continuous at a particular point if there is no break in its graph at that point.

If temperature represents a continuous function, what kind. Mathematically, f(x) is said to be continuous at x = a if and only if limₓ → ₐ f(x) = f(a). There are three types of discontinuities:

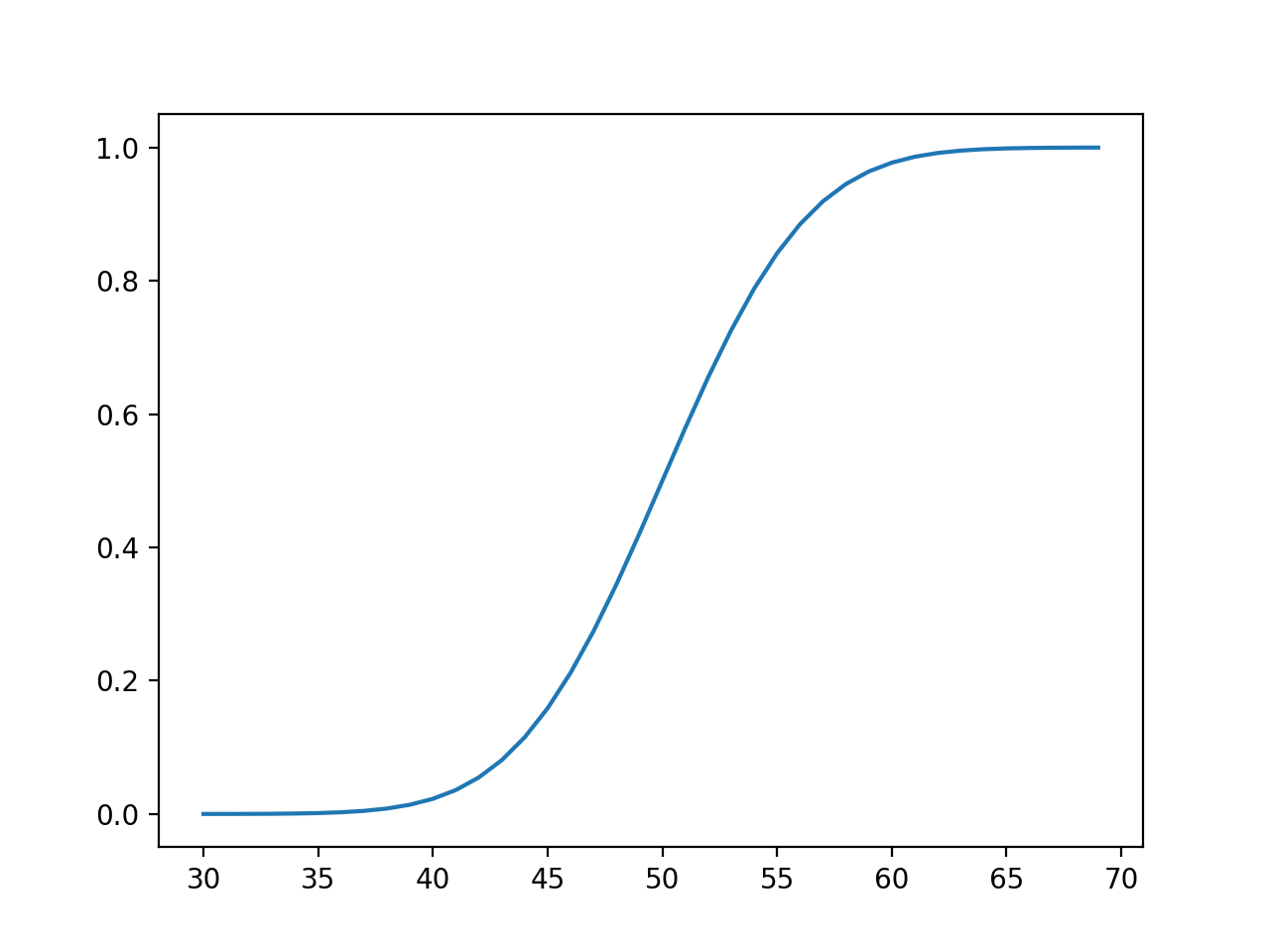
A function is continuous on an interval if we can draw the graph from start to finish without ever once picking up our pencil. Such functions are called continuous. This means that there are no gaps, breaks, or jumps in the line or curve, allowing for a smooth and unbroken representation of the data.

One way to test this informally is to trace/draw graph of the function; 10.1039/d4ta90115k this article is licensed under a. Continuous graphs are graphs where there is a value of y for every single value of x, and each point is immediately next to the point on either side of it so that the line of the graph is uninterrupted.