Peerless Tips About How Do You Know If A Line Is Good Fit For Residual Plot Graph Of Mean And Standard Deviation

Also, the points on the residual plot.

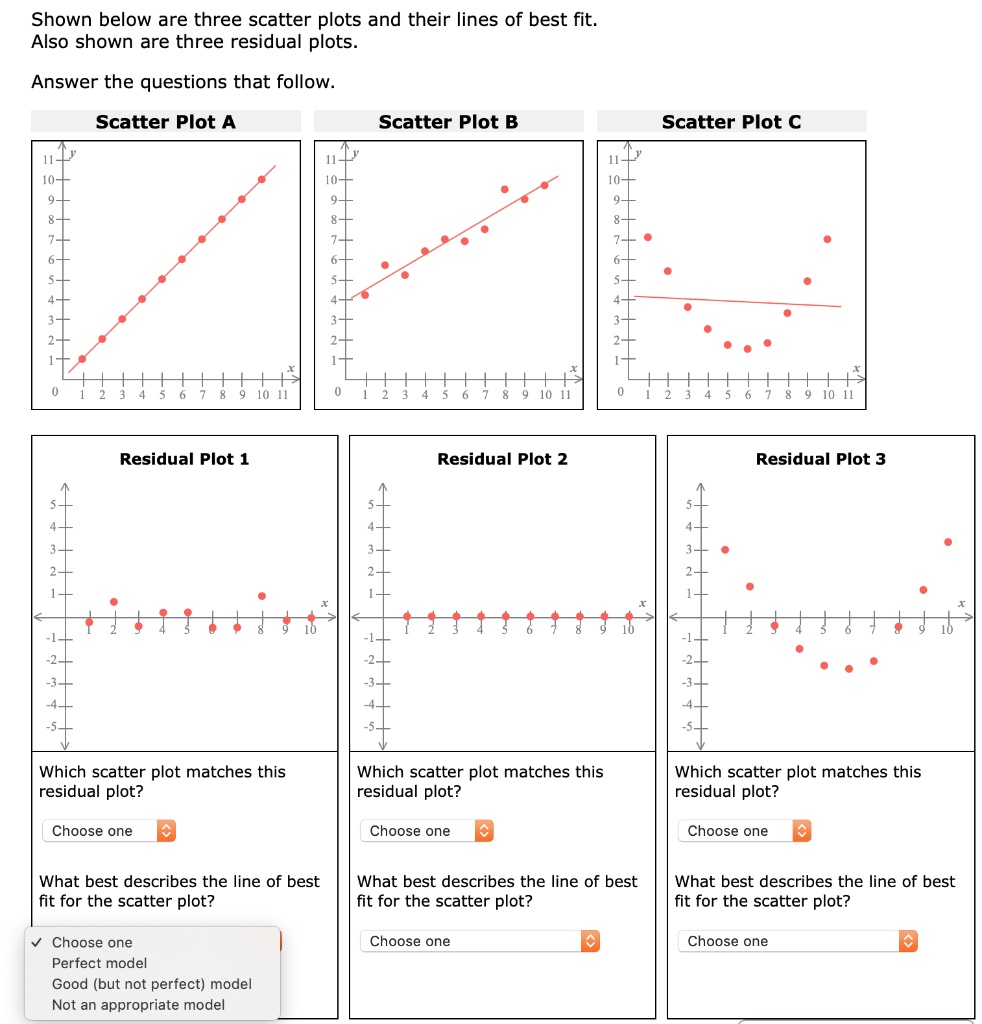
How do you know if a line is a good fit for a residual plot. Use scatterplot or component plus residual plot to examine the linear. The ideal random pattern of the. When conducting a residual analysis, a residuals versus fits plot is the most frequently created plot.

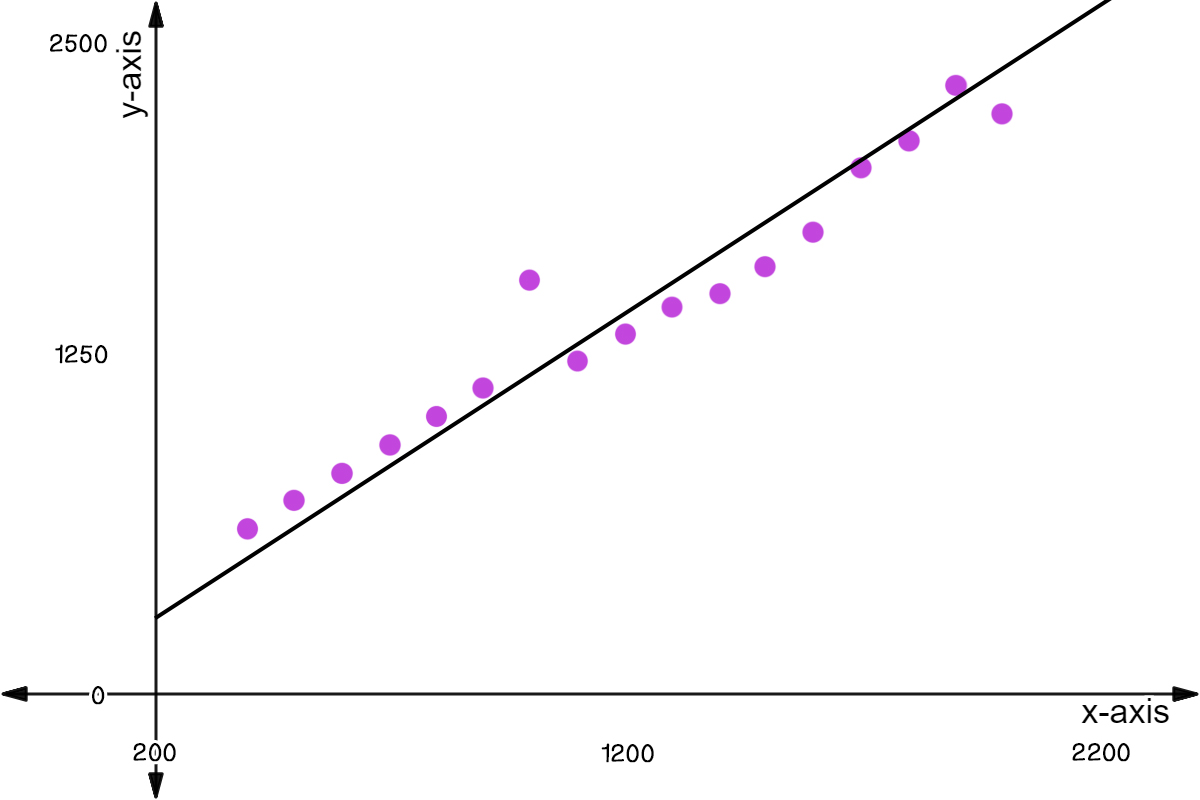
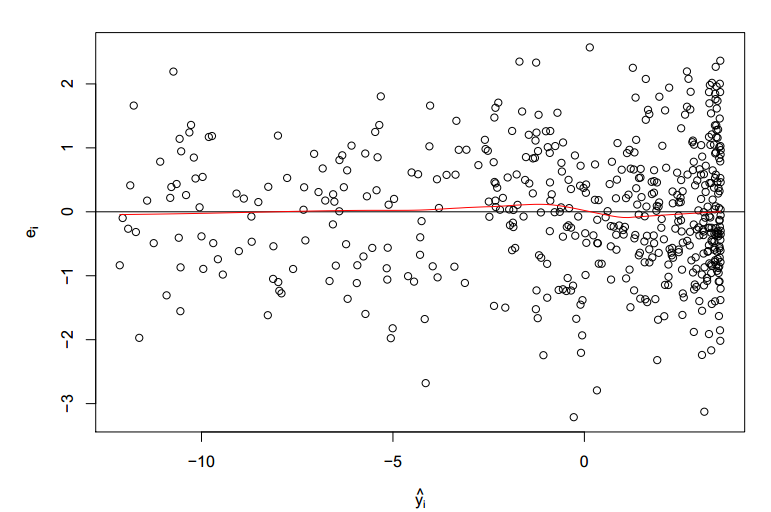
Residuals are the leftover variation in the data after accounting for the model fit: The first plot seems to indicate that the residuals and the fitted values are uncorrelated, as they. If the scatter plot indicates that there is a linear relationship between the variables, then.

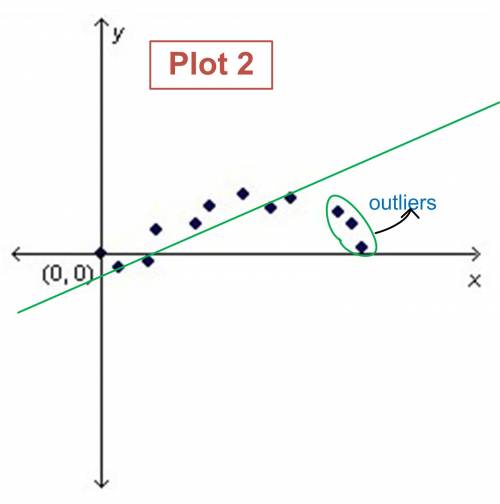
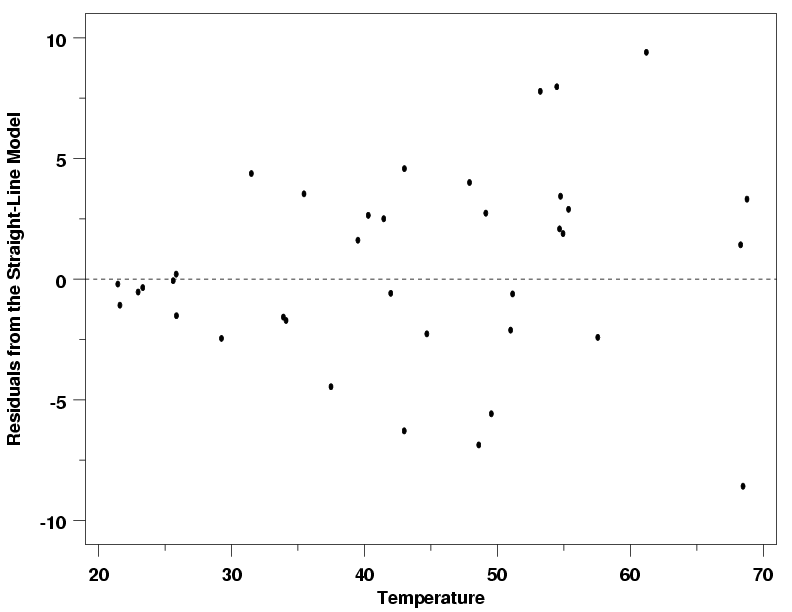
Do the residuals exhibit a clear pattern? If the residuals are randomly scattered around the horizontal axis, it indicates that the model is a good fit. It is a scatter plot of residuals on the y.

Residuals are helpful in evaluating how well a linear model fits a data set. But here are some that i would suggest you to check: Here's what the residual vs.

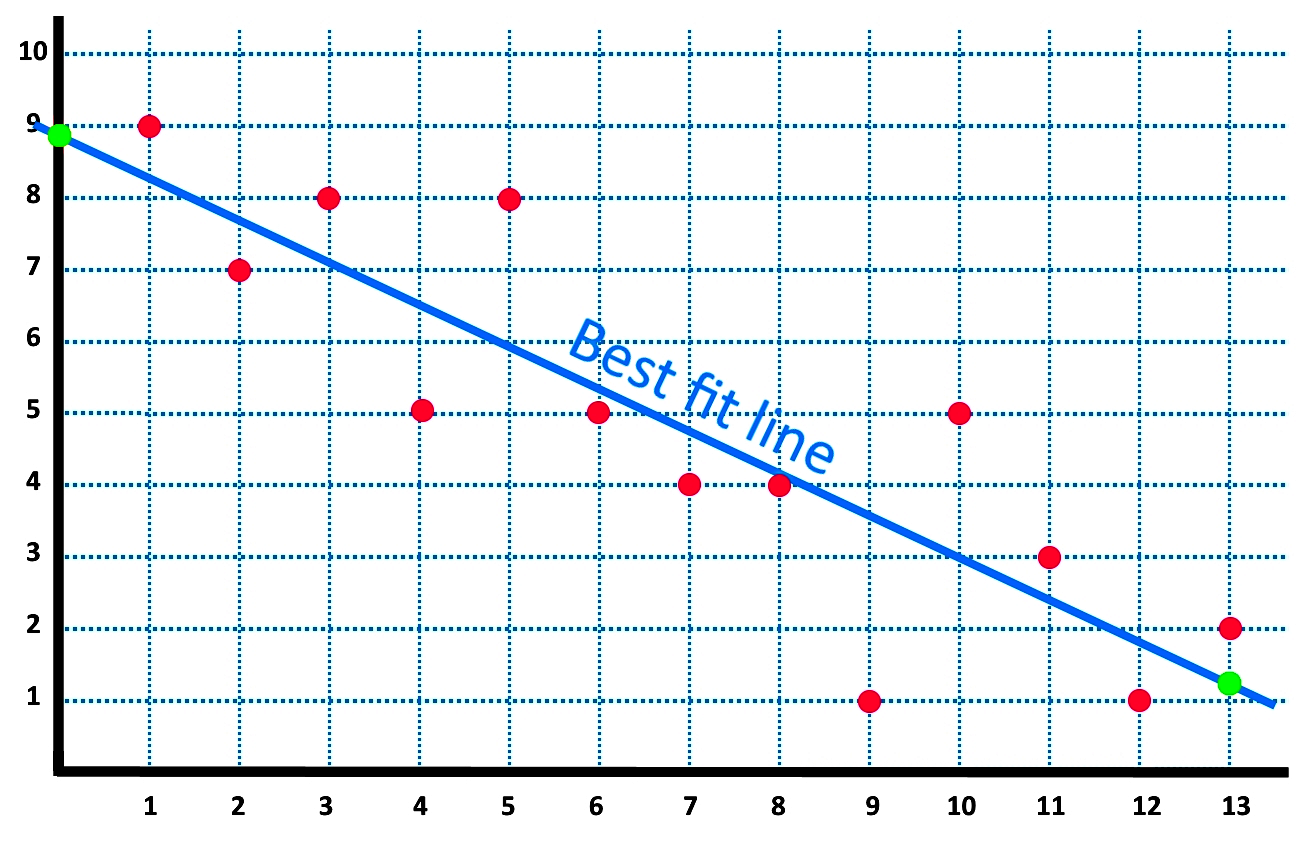
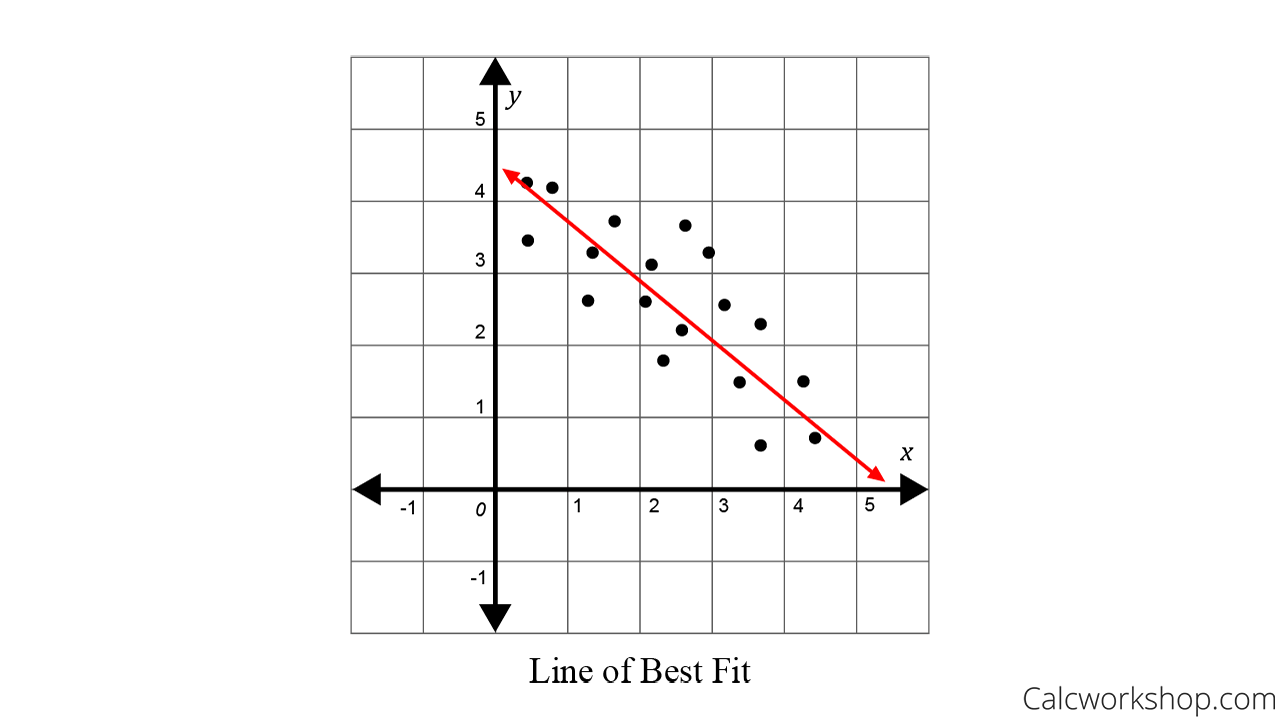
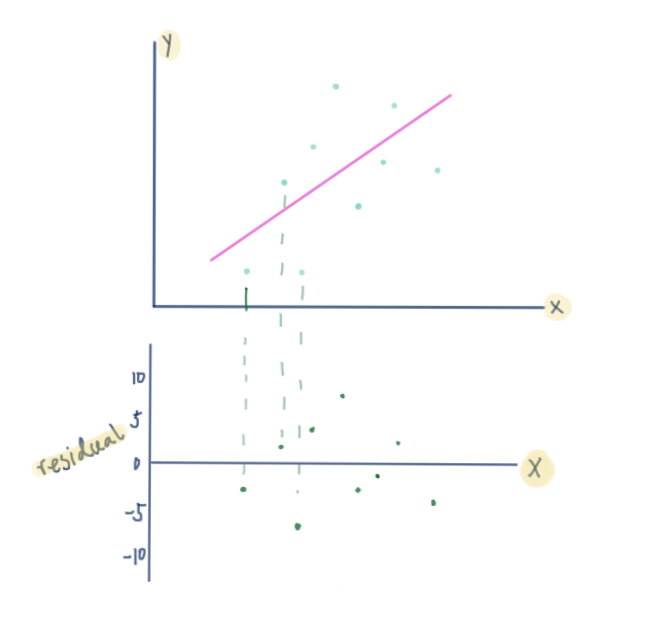
The green line on the scatter plot is the linear regression line of best fit. We often display them in a residual plot such as the one shown in figure. Figure 1 is an example of how to visualize residuals against the line of best fit.

The answer is, regardless of whether the regression line is upward sloping or downward sloping, this gives you a sense of how good a fit it is and whether a line is good at explaining the relationship between the variables. A residual plot has the residual. We can answer the following two questions to determine if this is a “good” residual plot:

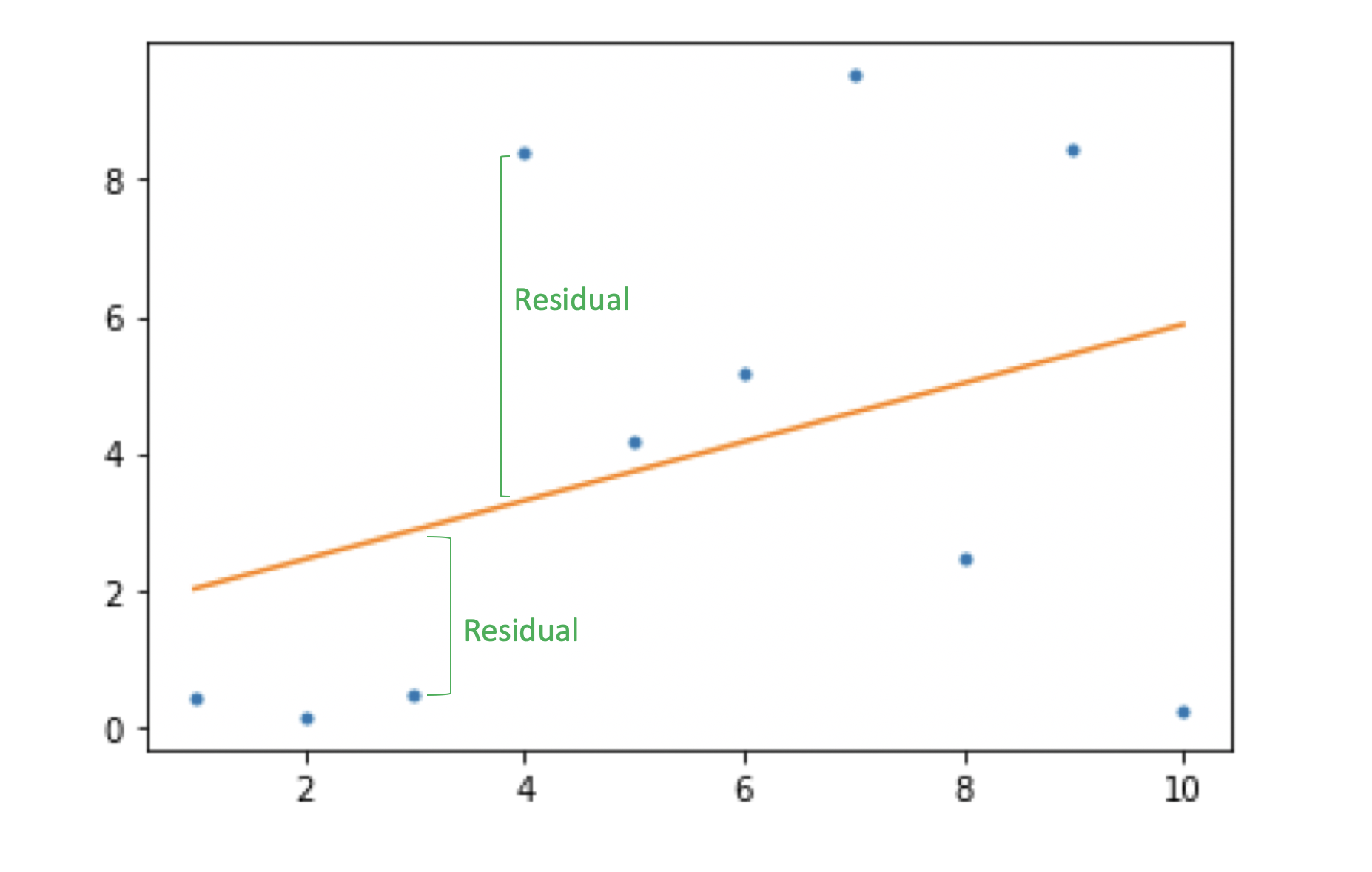
The vertical lines are the residuals. Do the residuals increase or. However, if there are visible patterns or trends in.

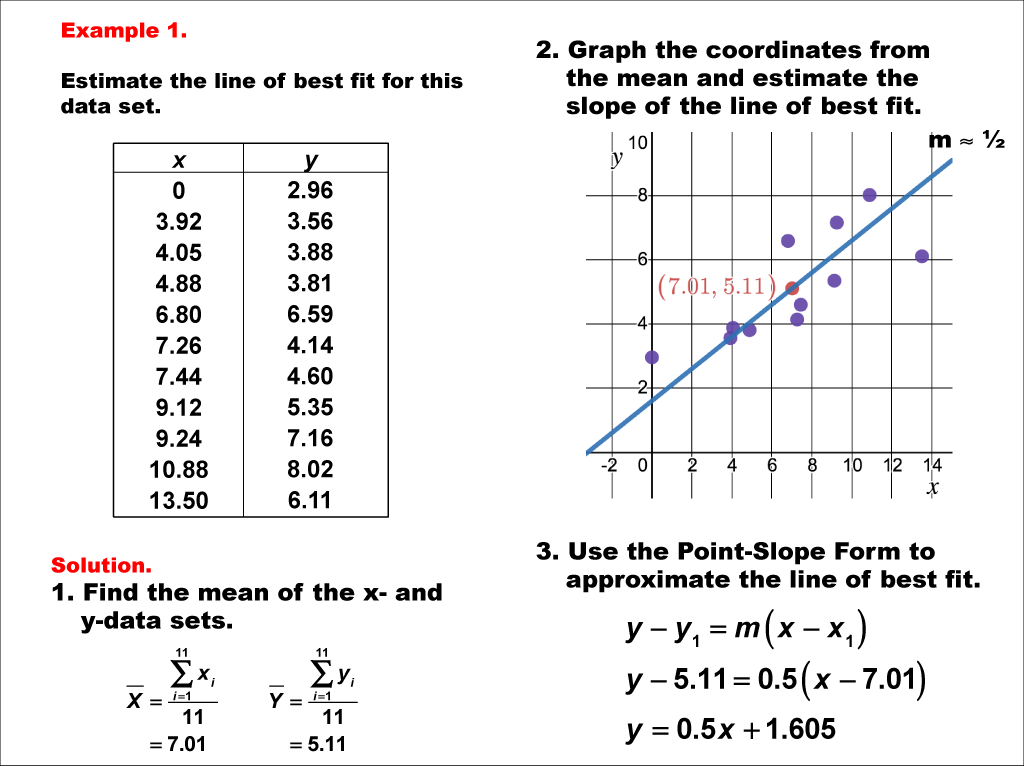
You can think of the lines as averages; Remember, it is always important to plot a scatter diagram first. In order to see whether a line is a good fit or a bad fit for a set of data we can examine the residuals of that line.

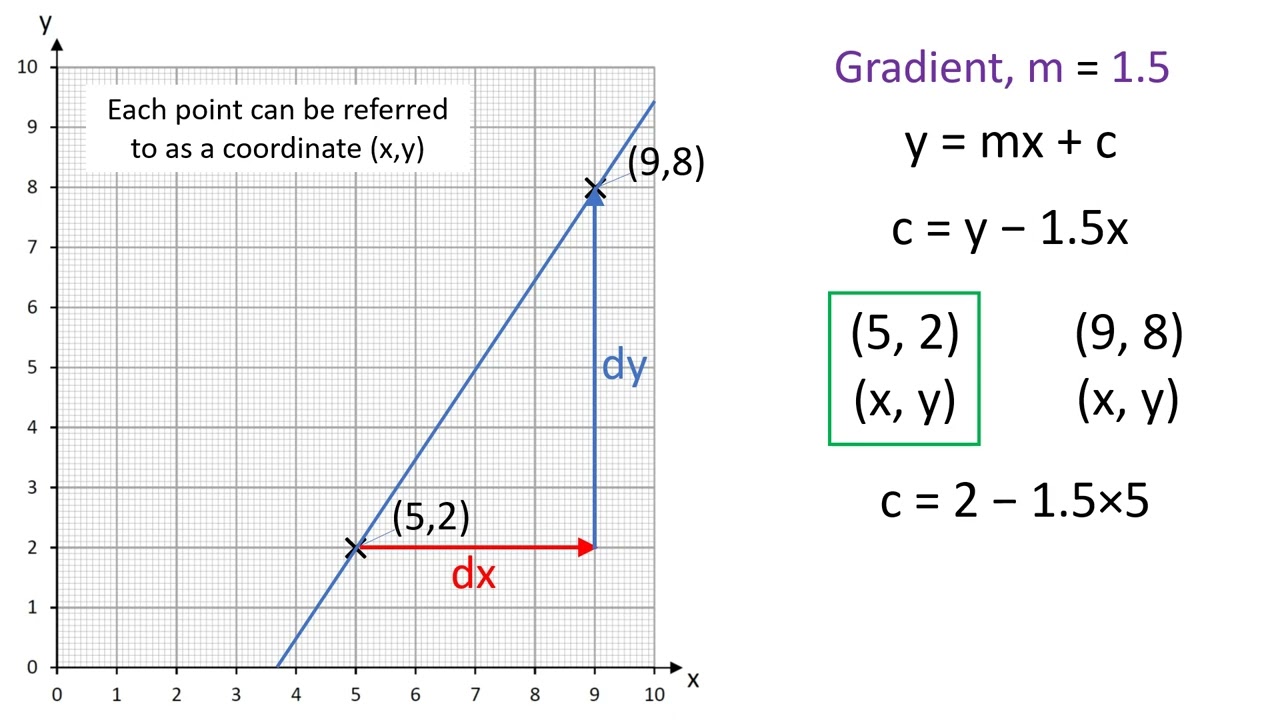
For example, the residual for the point ( 4 , 3 ) ‍ is − 2 ‍ : A few data points will fit the line and others will miss. Regression lines are the best fit of a set of data.

Suppose we fit a regression model and end up with the following residual plot: The residuals are randomly scattered about zero with no clear pattern. \[\text {data} = \text {fit + residual}\] each observation will have a residual.