Exemplary Info About What Is A Smooth Parametric Curve Add Trendline Excel Chart

What is a smooth parametric curve. The algorithm for identifying whether or not a parametric curve is smooth contains a first step of finding out when dx/dt and dy/dt is simultaneously 0. 7.2.2 find the area under a parametric curve. As we've seen, the idea of parametric curves is very simple:

Next, i wish to define smoothness for a parameterised curves. For the sake of this discussion, a curve is smooth at a point $x$ if $f'(x)$ exists. Instead of specifying y as a function of x (or x as a function of y), we give both x and y as functions.

We’ll use parametric curves where the functions are all polynomials in the parameter. These values, along with the two arrows along the curve, are. Simply put, a parametric curve is a normal curve where we choose to define the curve's x and y values in terms of another variable for simplicity or elegance.

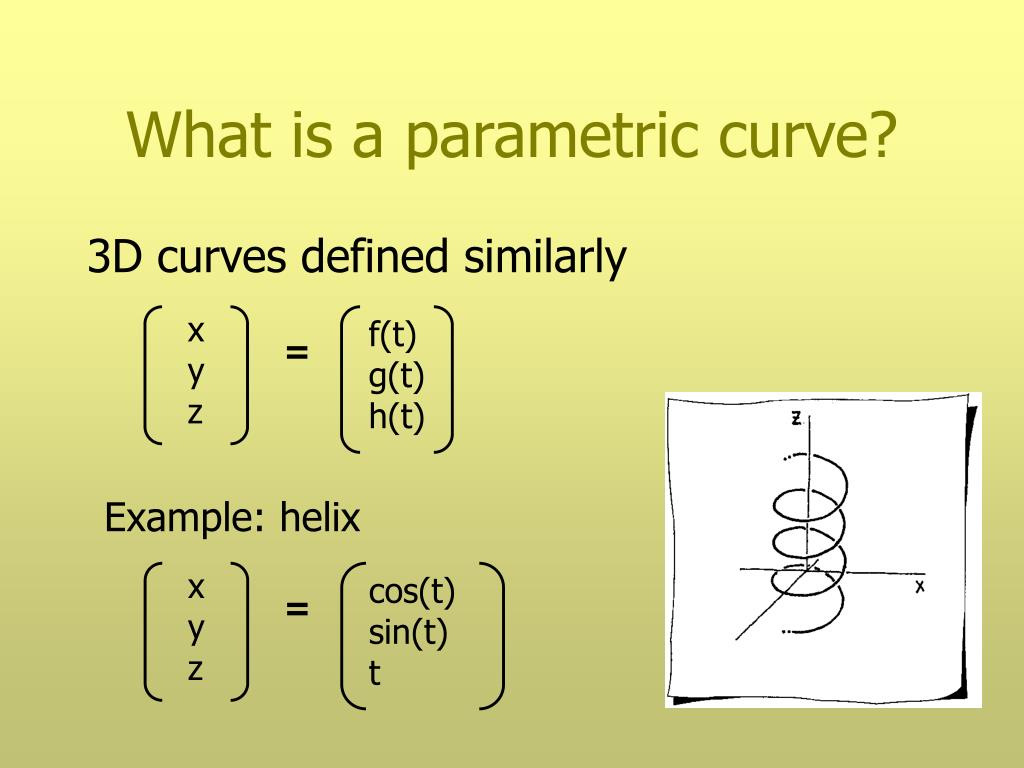
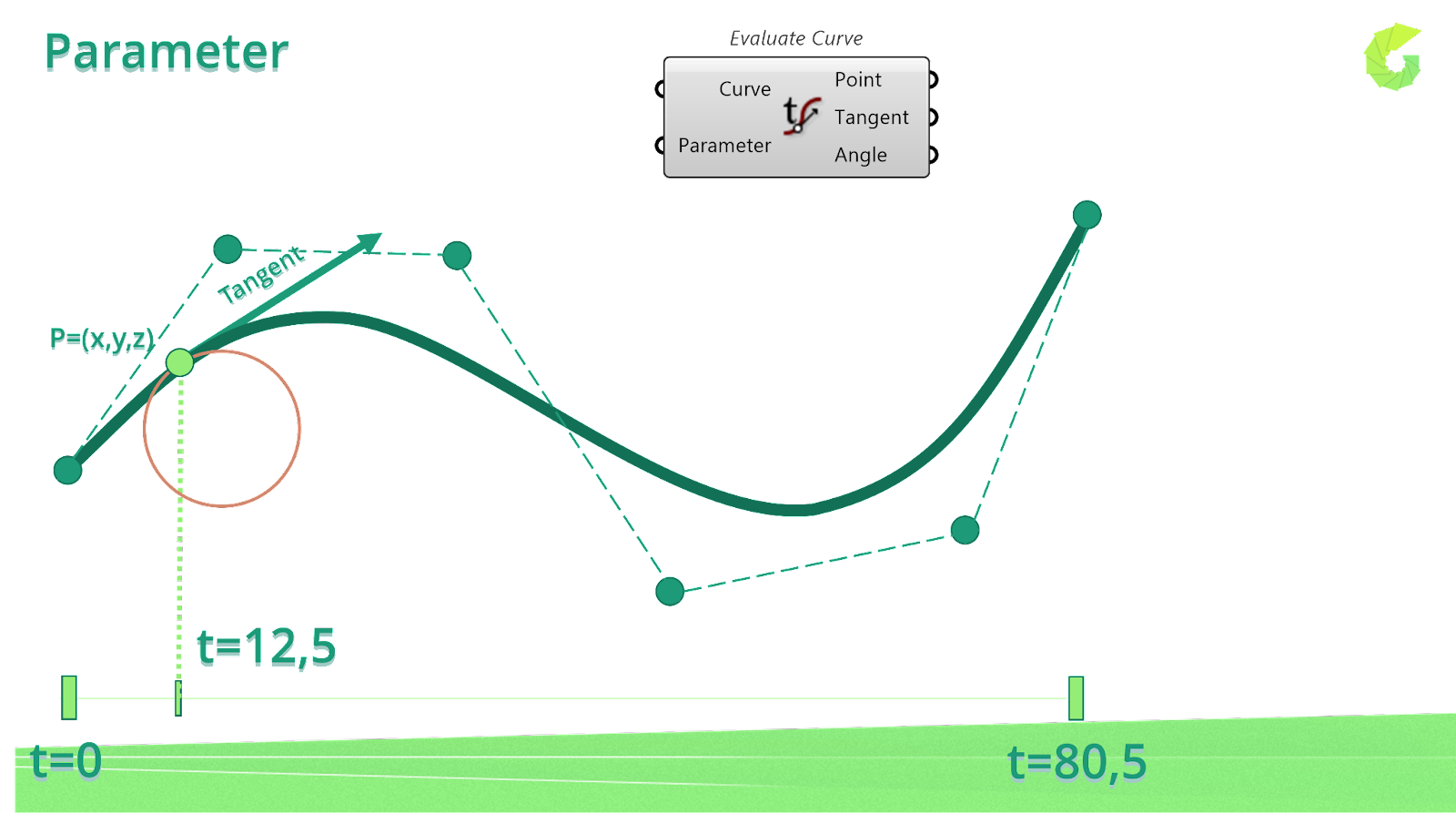
Converting from rectangular to parametric can be very simple: In this section we want to briefly discuss the curvature of a smooth curve (recall that for a smooth curve we require →r ′(t) r → ′ ( t) is continuous and →r ′(t) ≠ 0 r. In this section we will introduce parametric equations and parametric curves (i.e.

A smooth curve is any curve for which r ˙(t) r → ˙ ( t) is continuous and r ˙(t) ≠ 0 r → ˙ ( t) ≠ 0 for any t t except possibly at the endpoints. Determine derivatives and equations of tangents for parametric curves. We will graph several sets of parametric.

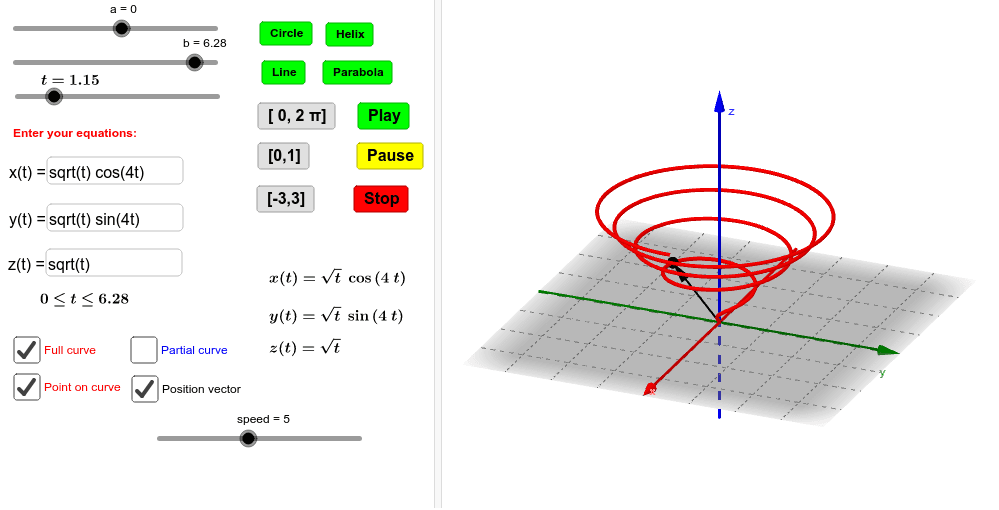
Never the less, we know that most curves are written in parametric equations in terms of some dummy variable, most commonly \(t\). We only consider smooth simple curves in our course or the curves which can be decomposed. Given y = f(x) y = f(x), the parametric equations x = t x = t, y = f(t) y = f(t) produce the same graph.

Notice in this definition that \(x\) and \(y\) are used in two. Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the. 7.2.3 use the equation for arc length of a parametric.

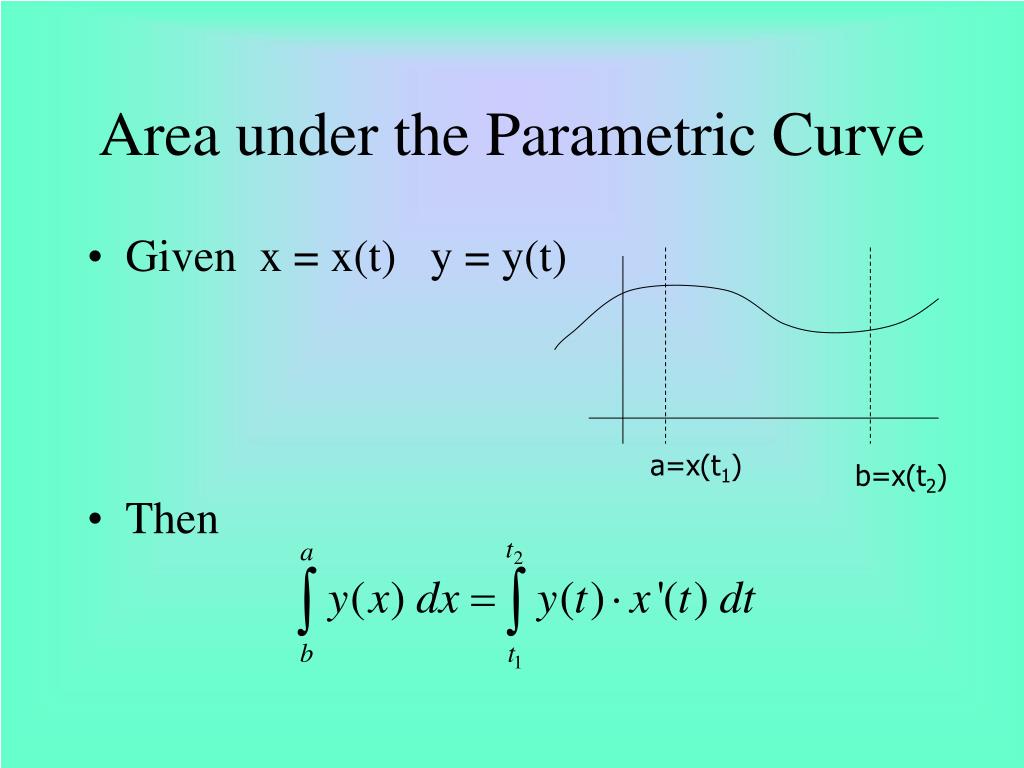
This looks to me very. Find the area under a parametric curve.

By definition, a parameterised smooth curve in $\mathbb{r}^n$ is a smooth (i.e. Parametric equations define x and y as functions of a third. The graph of parametric equations is called a parametric curve or plane curve, and is denoted by \(c\).

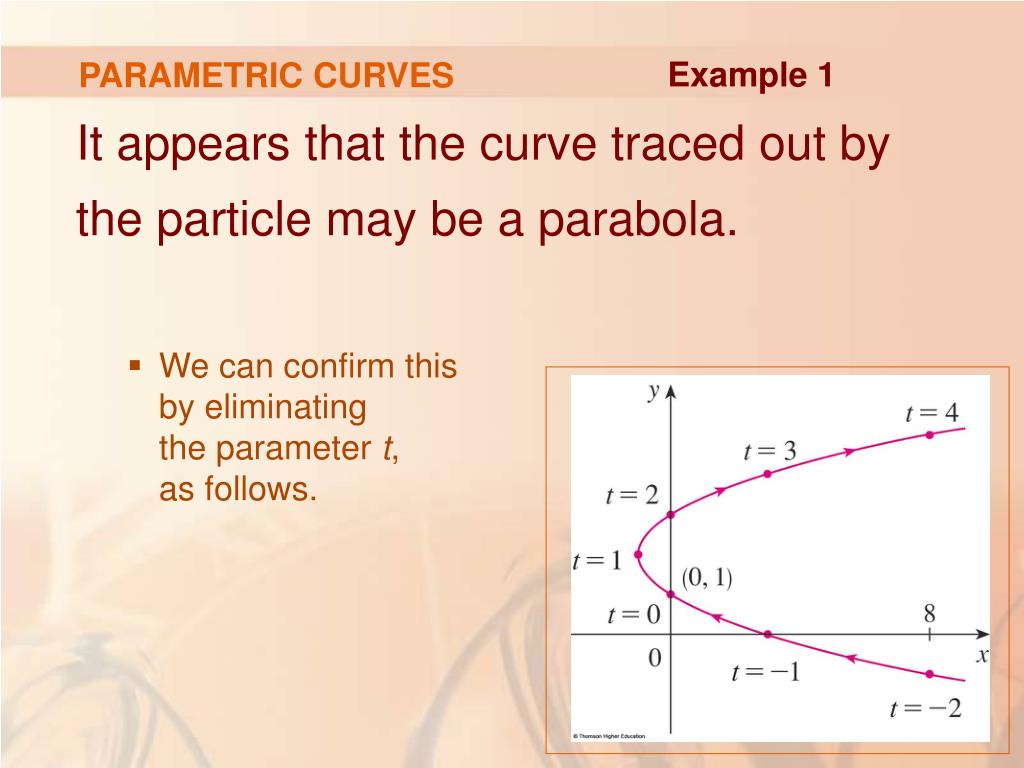
As an example, given y = x2 y = x. The points have been connected with a smooth curve. Recognize the parametric equations of.