Brilliant Strategies Of Info About Is Curve And Parabola The Same Adding Second Y Axis In Excel

Make a parabola by folding paper.

Is curve and parabola the same. A fixed straight line (the directrix) Each planet's orbit about the sun is an ellipse. From a point \(p\) on a parabola with vertex \(v\) let \(\overline{pq}\) be the line segment perpendicular to the axis at a point \(q\).

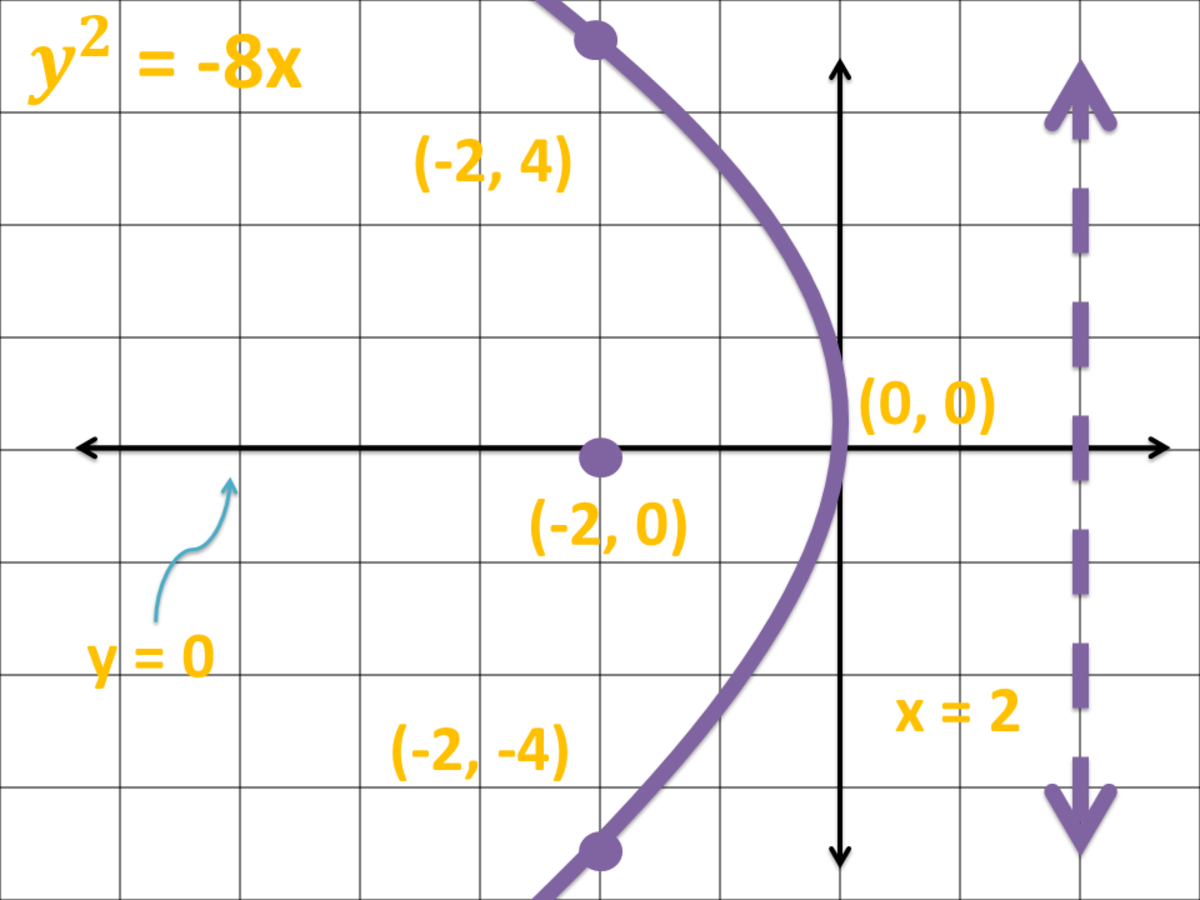
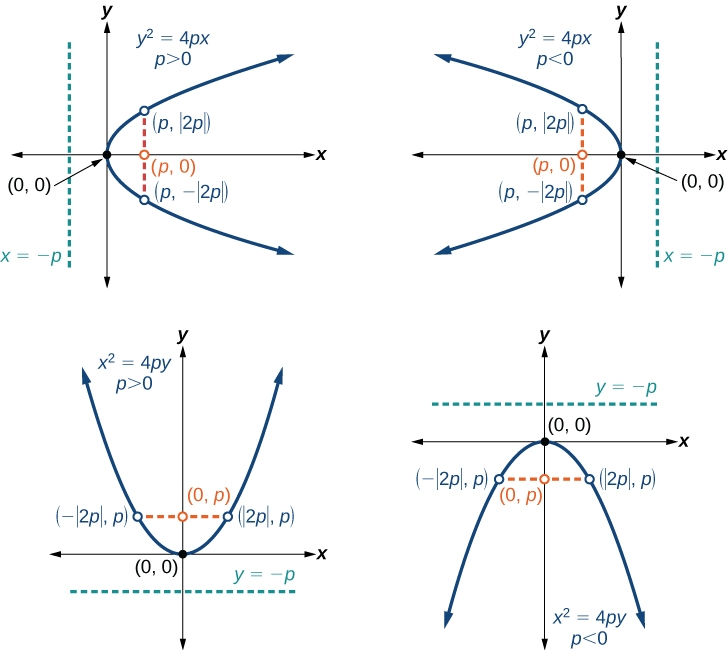
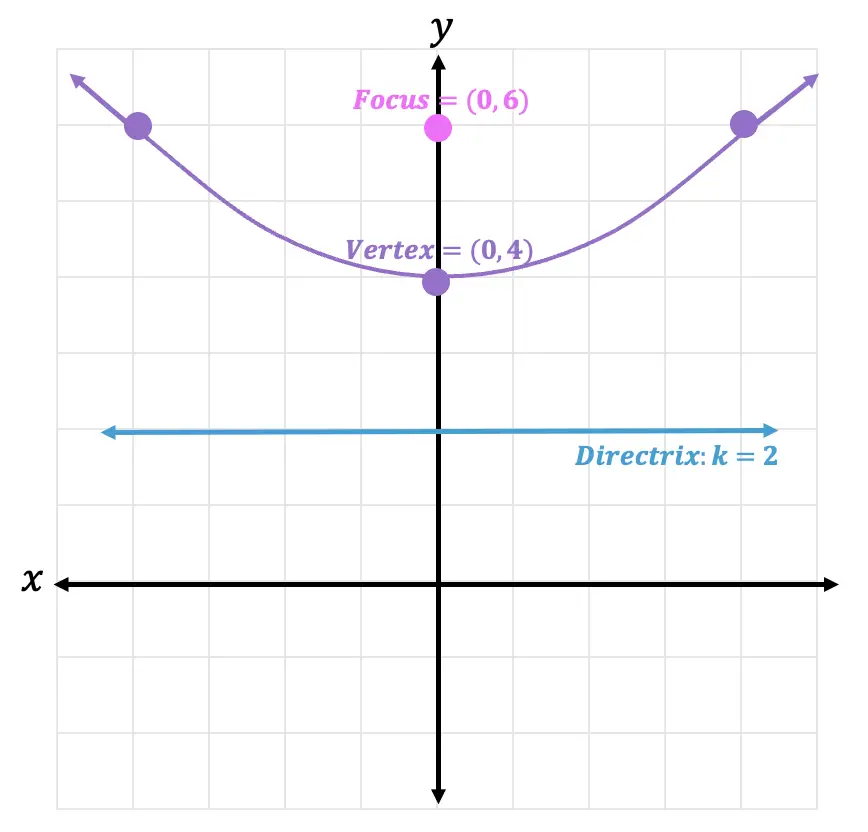
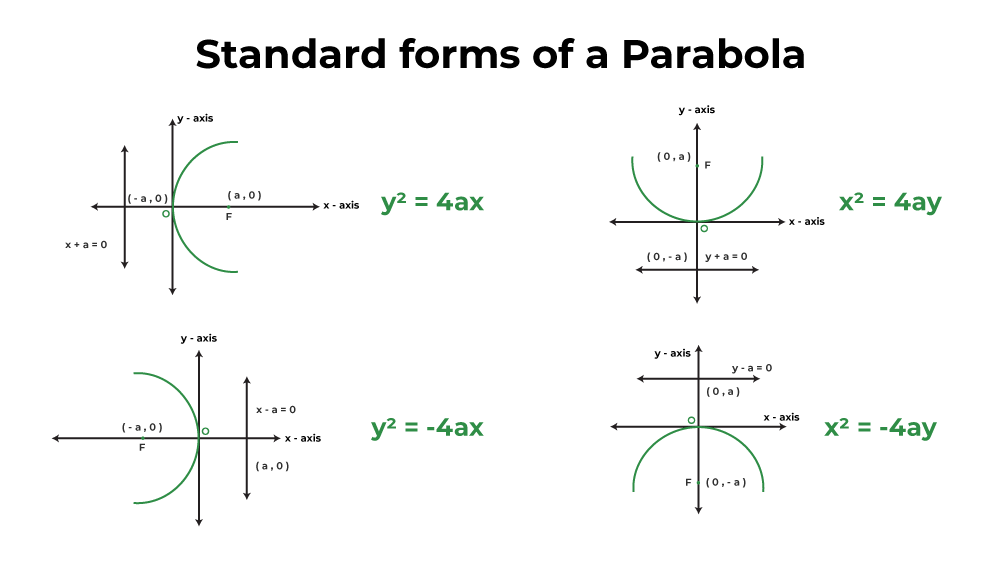
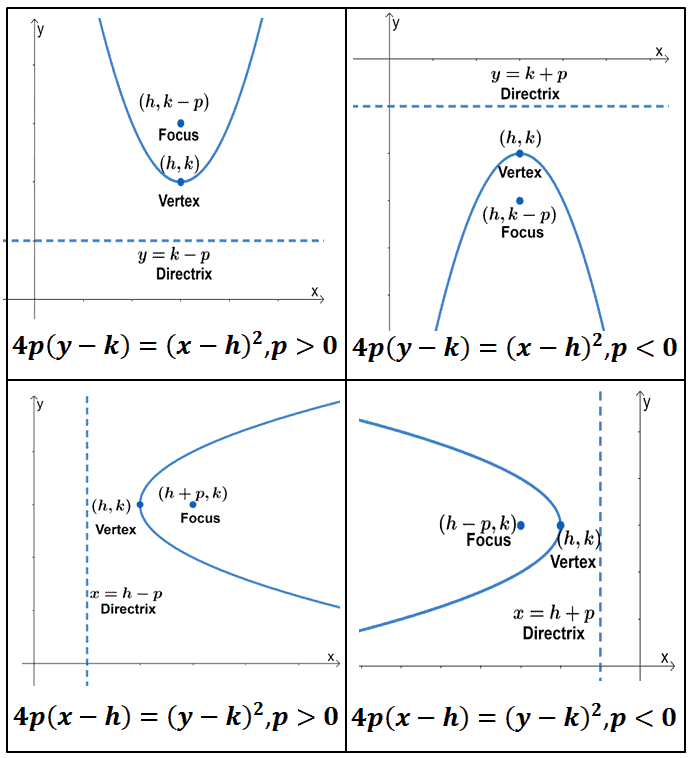
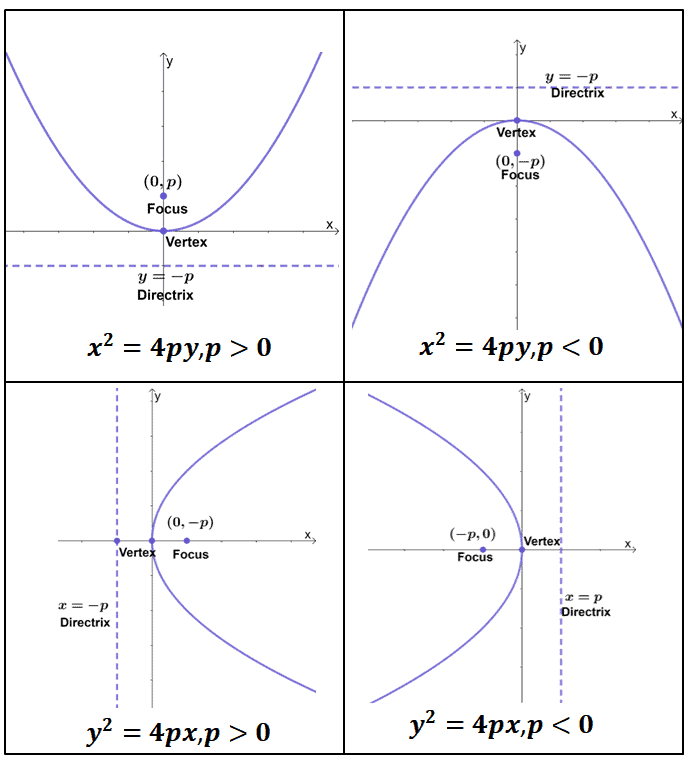
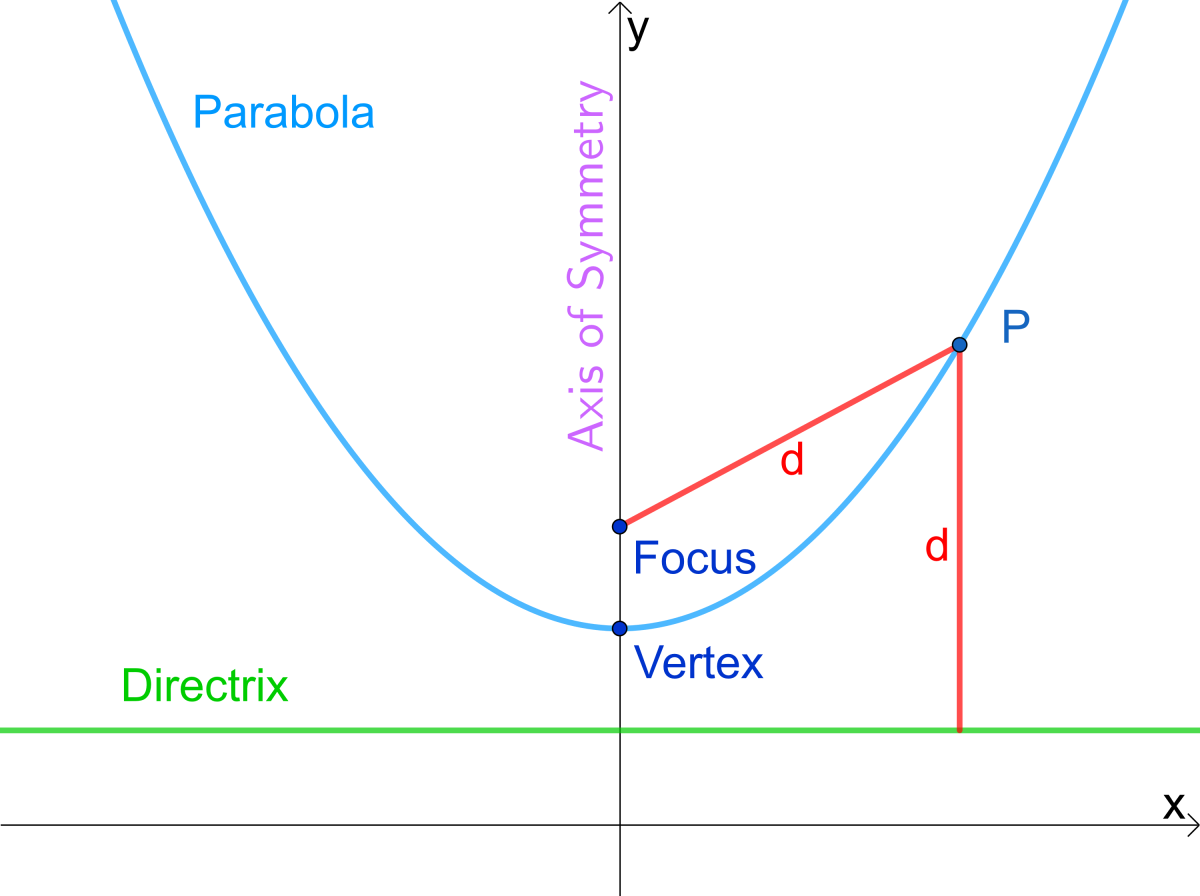
When given a standard equation for a parabola centered at the origin, we can easily identify the key features to graph the parabola. One description of a parabola involves a point (the focus) and a line (the directrix). A parabola is the set of all points[latex]\,\left(x,y\right)[/latex] in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix.

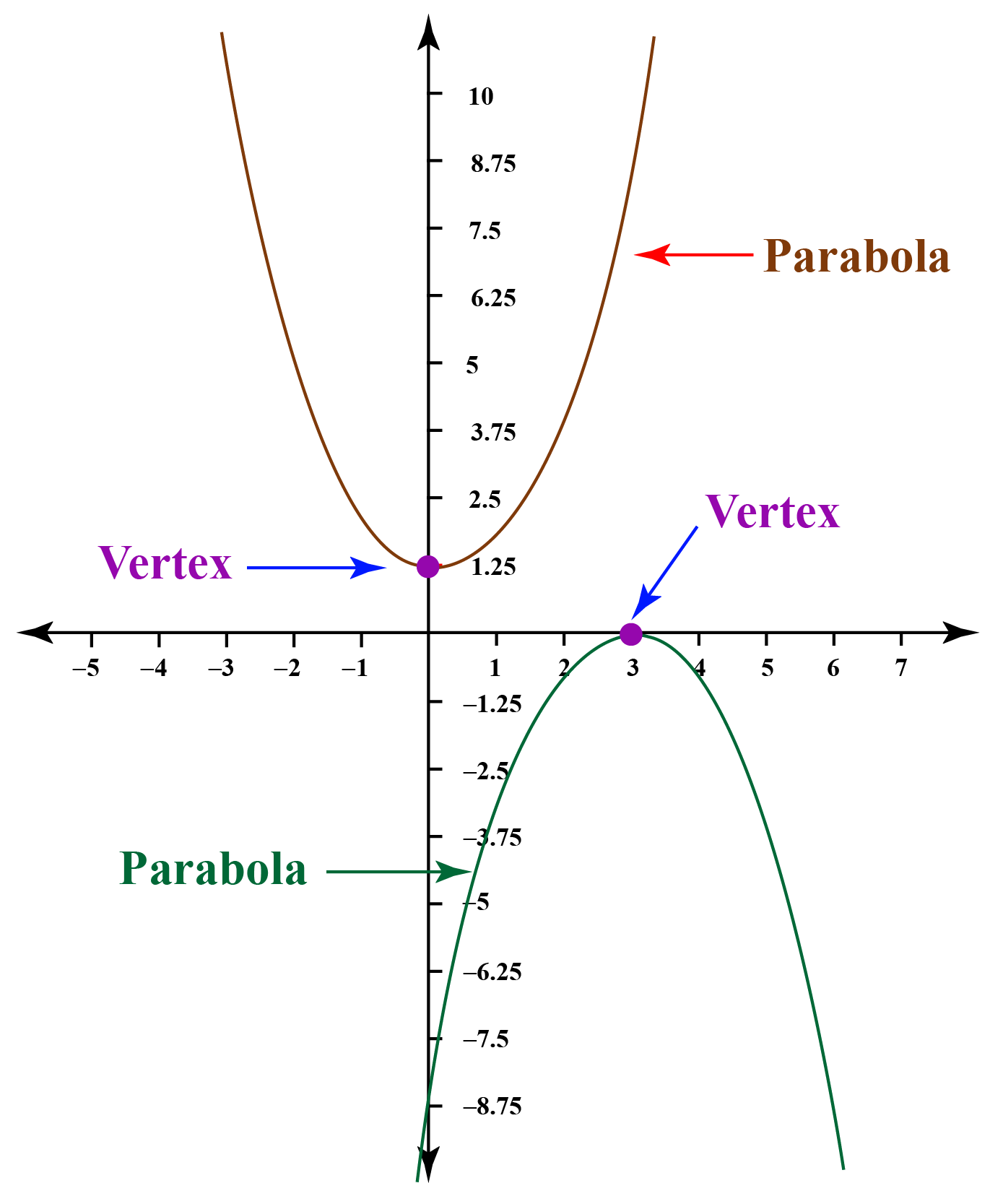
Some of them are opened upwards like this yellow one and this pink one, and some of them are open downwards. The parabola is the curve formed from all the points (x, y) that are equidistant from the directrix and the focus. Each dashed line from the point \(f\) to a point on the curve has the same length as the dashed line from the point on the curve to the line \(d\).

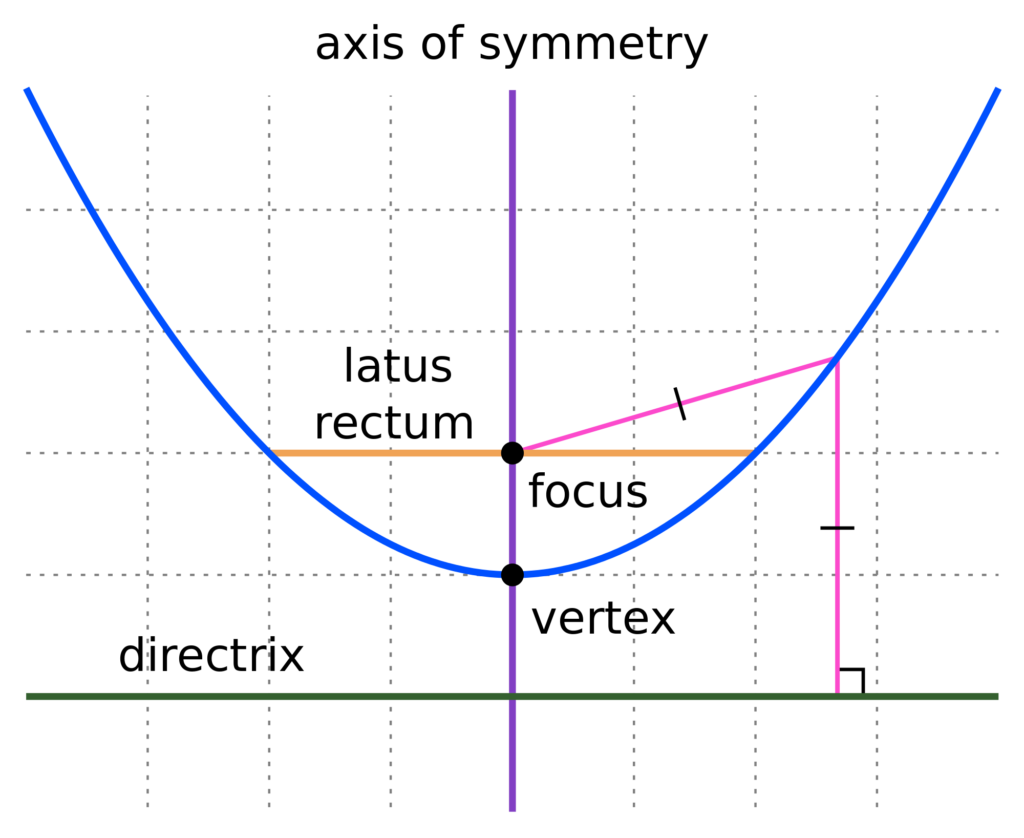
This parabola that opens upward shows that all points, $p$, along the parabola’s curve will share the same distance from the focus and the directrix. The point suggestively labeled \(v\) is, as you should expect, the vertex. So if you were to invert this, the horizontal parabola cannot be a function;

A parabola is a curve where any point is at an equal distance from: A line is said to be tangent to a curve if it intersects the curve at exactly one point. A segment of a parabola is a lissajous curve.

Here are some examples of parabolas. Parabola, open curve, a conic section produced by the intersection of a right circular cone and a plane parallel to an element of the cone. Show that \(pq^2\) equals the product of \(qv\) and the length of the latus rectum.

The graphs of quadratic functions are called parabolas. The sun's center is always located at one focus of the ellipse. A fixed point (the focus), and;

In the illustration below, the blue curve is a parabola and the red curve is a catenary. As a plane curve, it may be defined as the path of a point moving so that its distance from a fixed line is equal to its distance from a fixed point. In quadratic functions , we learned about a parabola’s vertex and axis of.

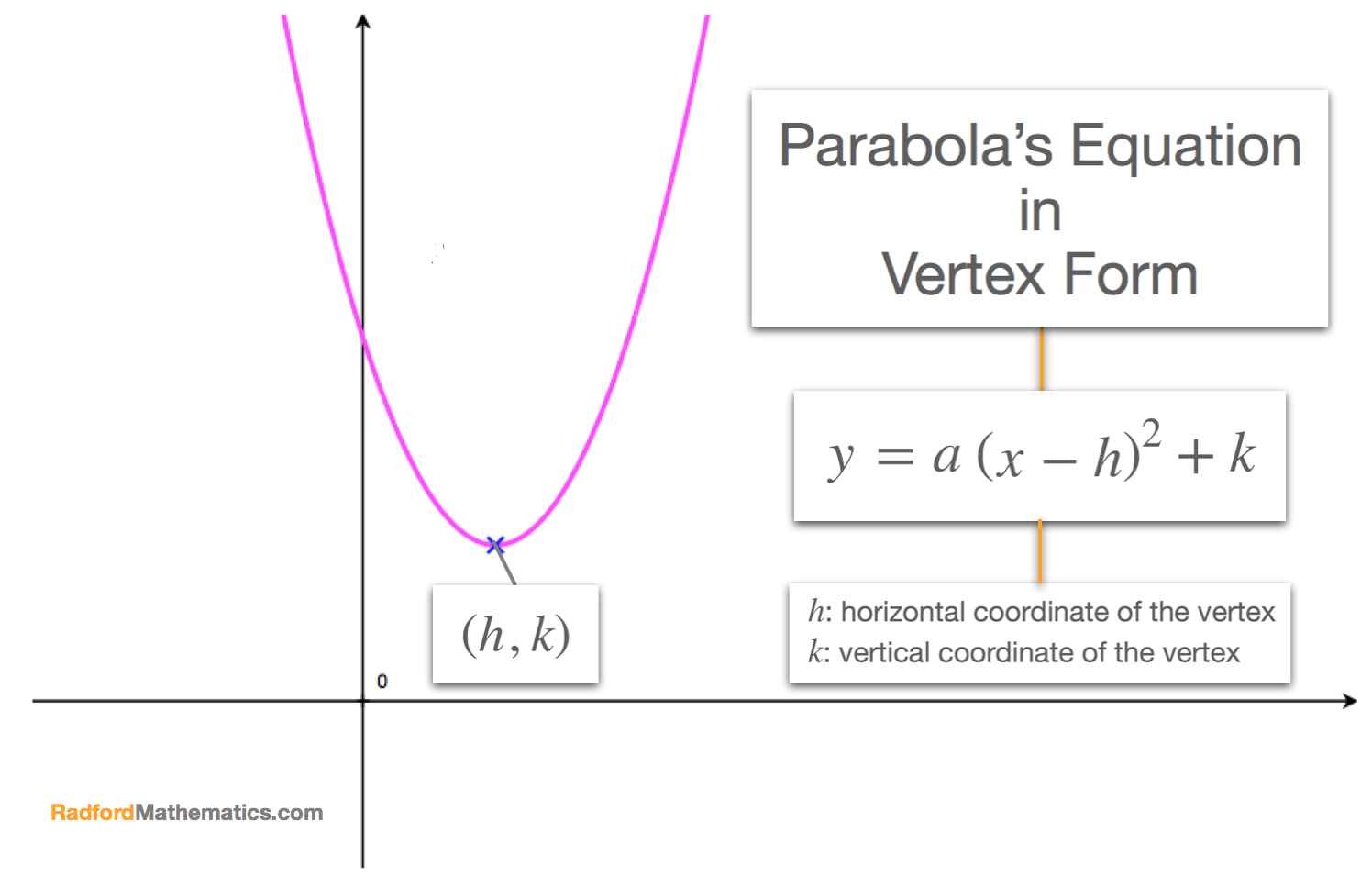
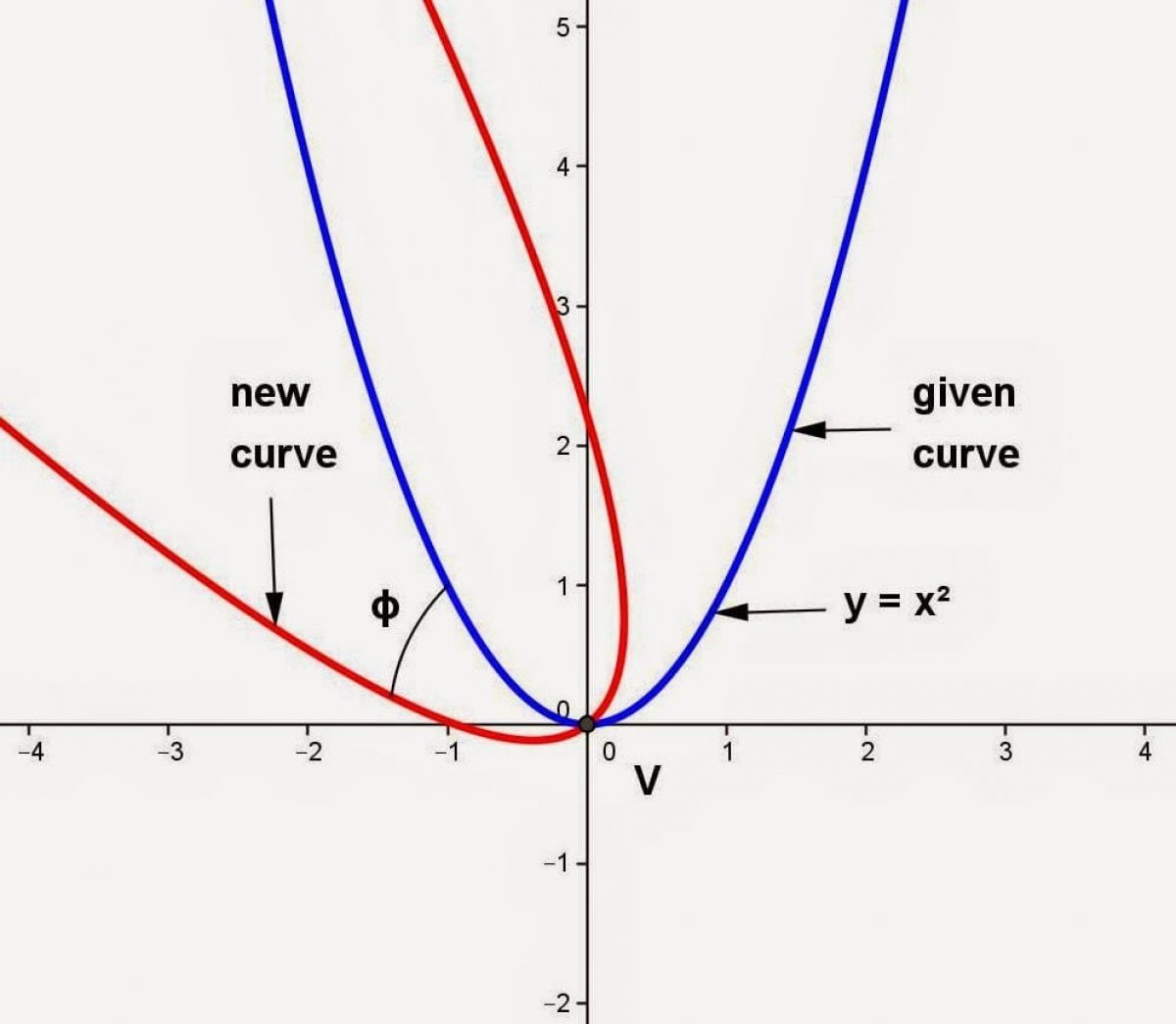
High school textbooks make the claim that a parabola is the same shape curve as the graph of a quadratic equation \(y=ax^2+bx+c\). A parabola will contain three important elements: A parabola is the set of all points \((x,y)\) in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix.

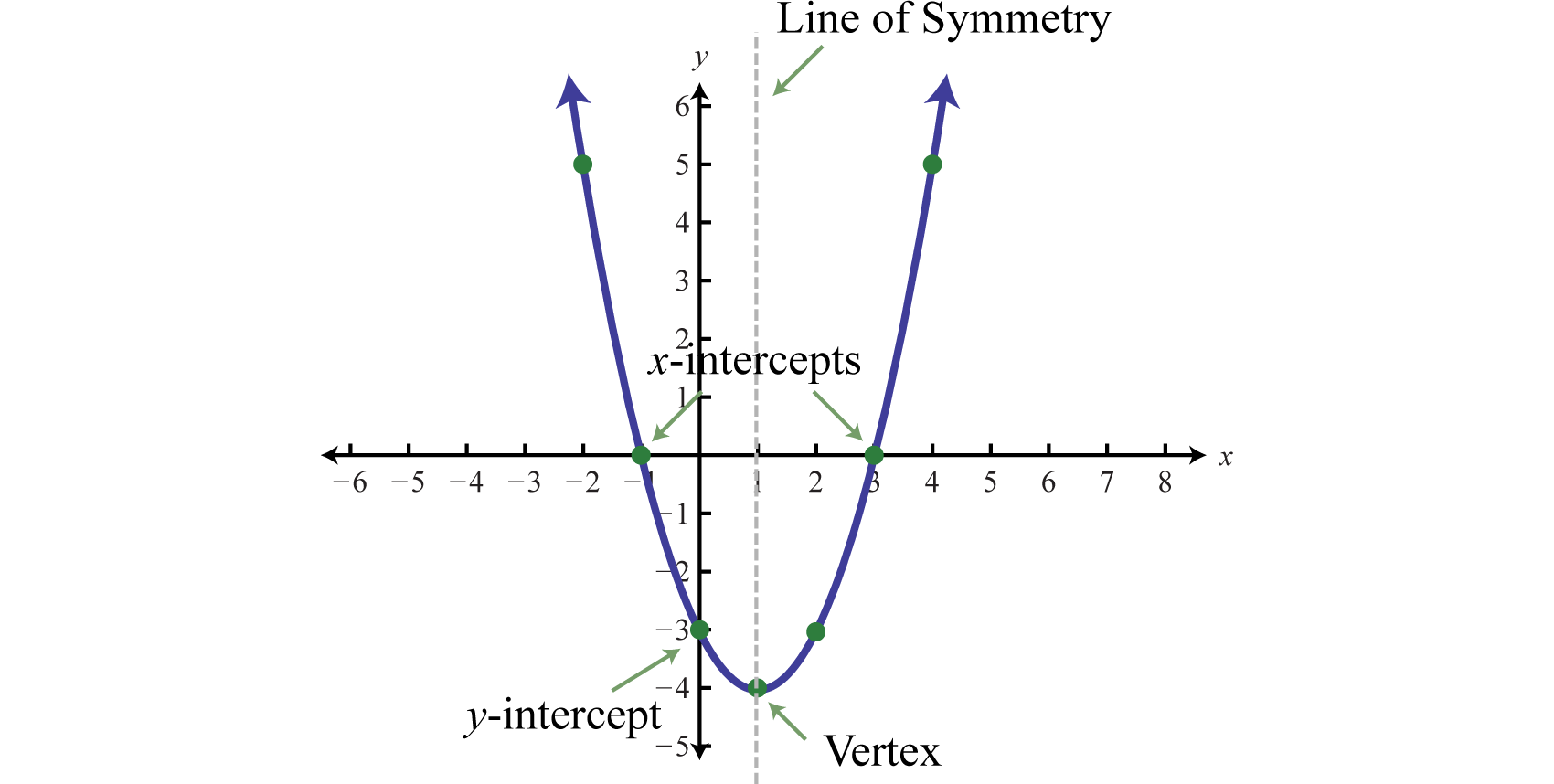
Mark off regular intervals along the bottom edge and measures heights from the bottom edge to the curve as shown. A focus, a directrix, and a vertex. In this section we want to look at the graph of a quadratic function.