Unbelievable Info About How Do You Create A Linear System Latex Line Chart

But why would we ever want to do this?

How do you create a linear system. If you don't have equations where you can eliminate a variable by addition or subtraction you directly you can begin by multiplying one or both of the equations with a constant to obtain an equivalent linear system where you can eliminate one of the variables by addition or subtraction. Let us look more closely at one example: These are all linear equations:

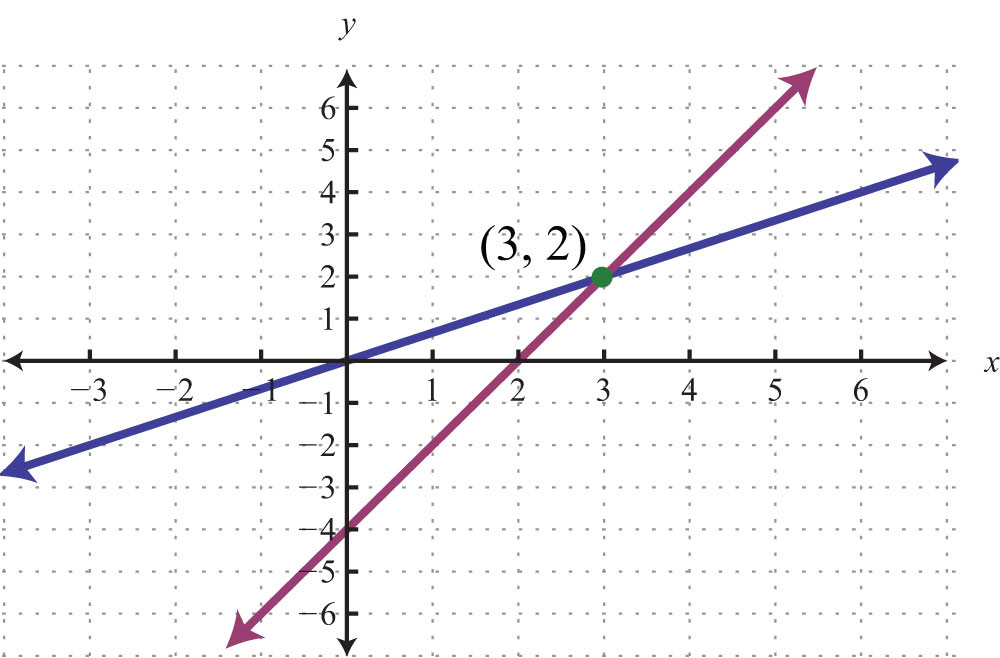
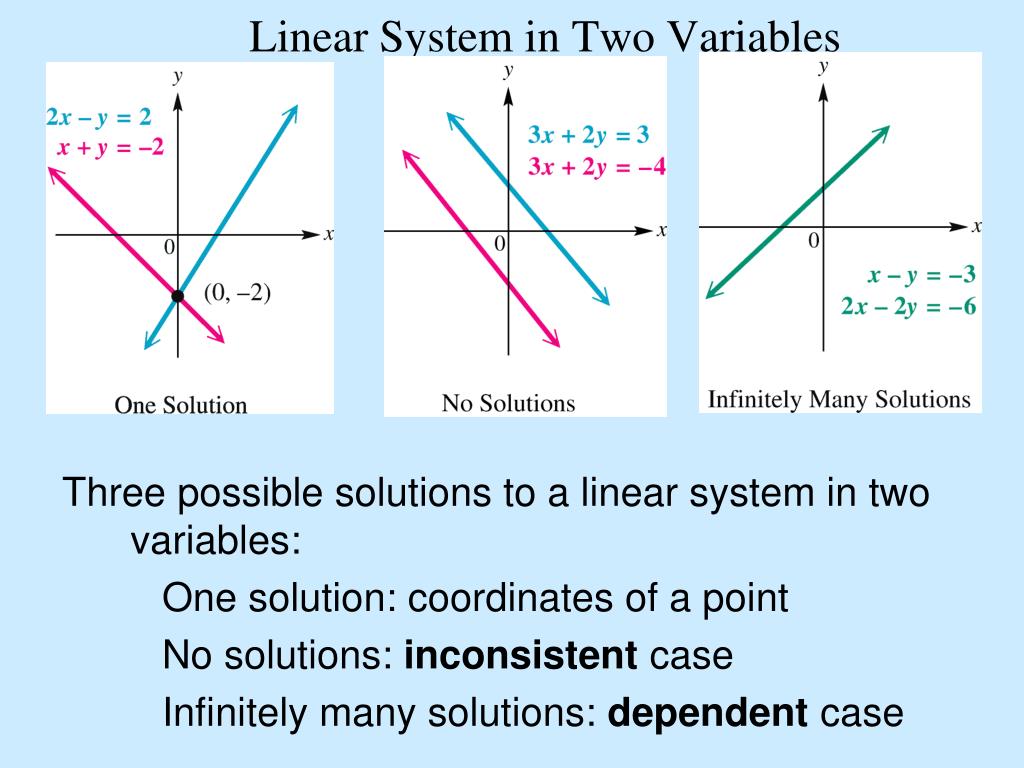
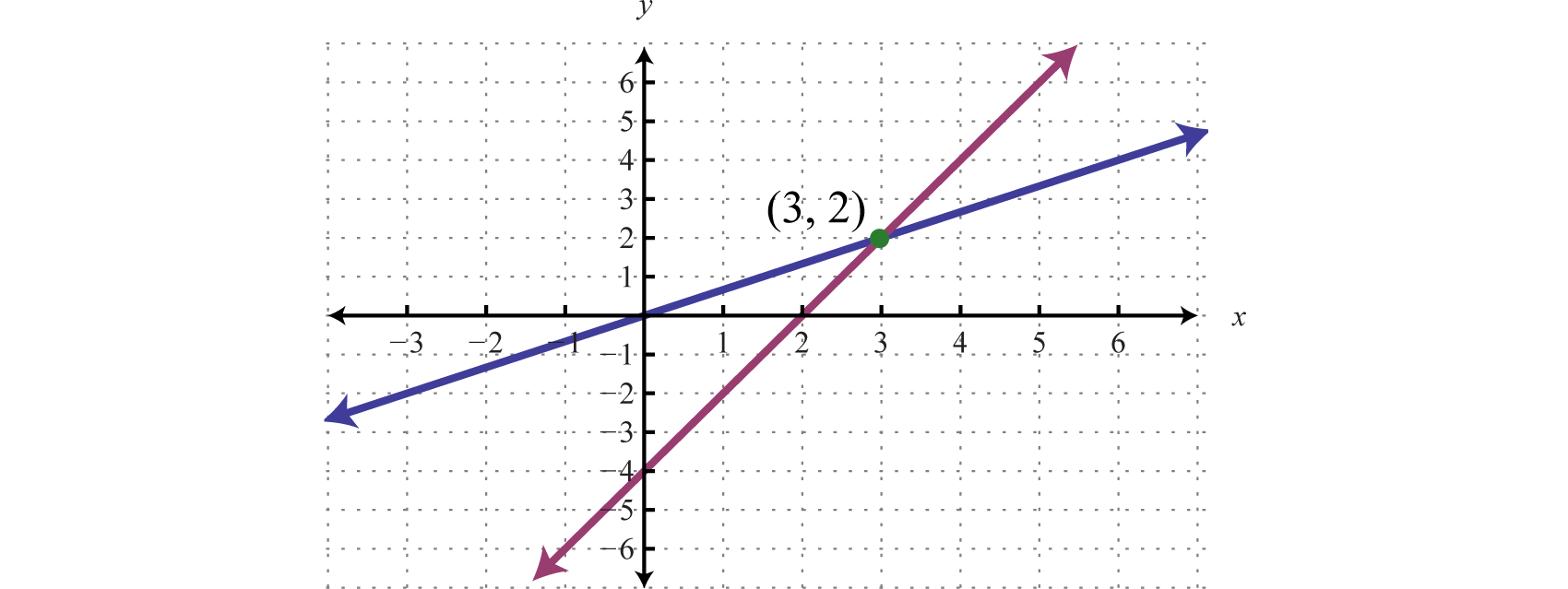
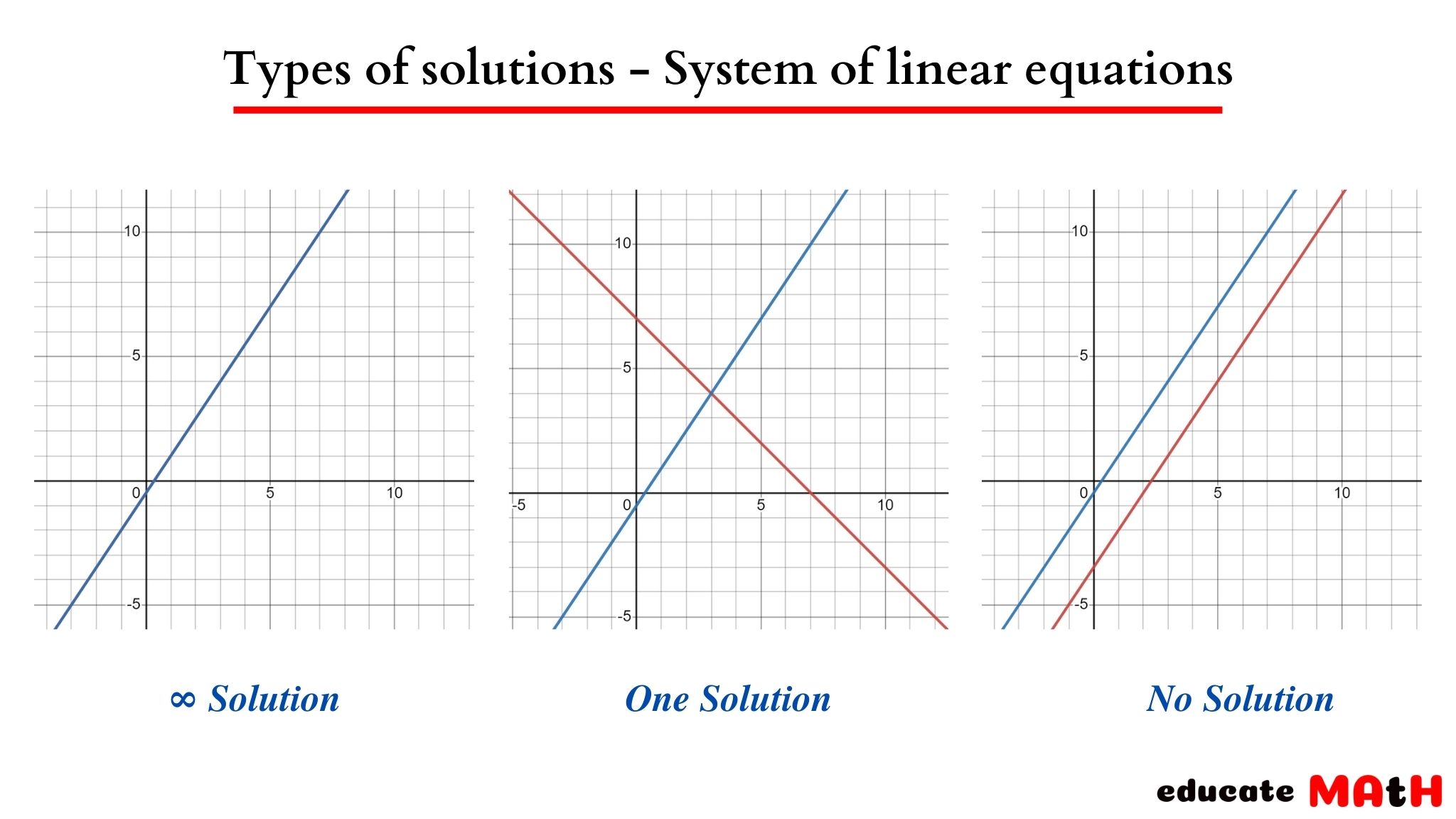
The image below summarizes the 3 possible cases for the solutions for a system of 2 linear equations in 2 variables. In the first equation, the coefficient of both variables is 1 1. For example, a solution to a linear system, or simultaneous solution, to a linear system is an ordered pair \((x, y)\) that solves both of the equations.

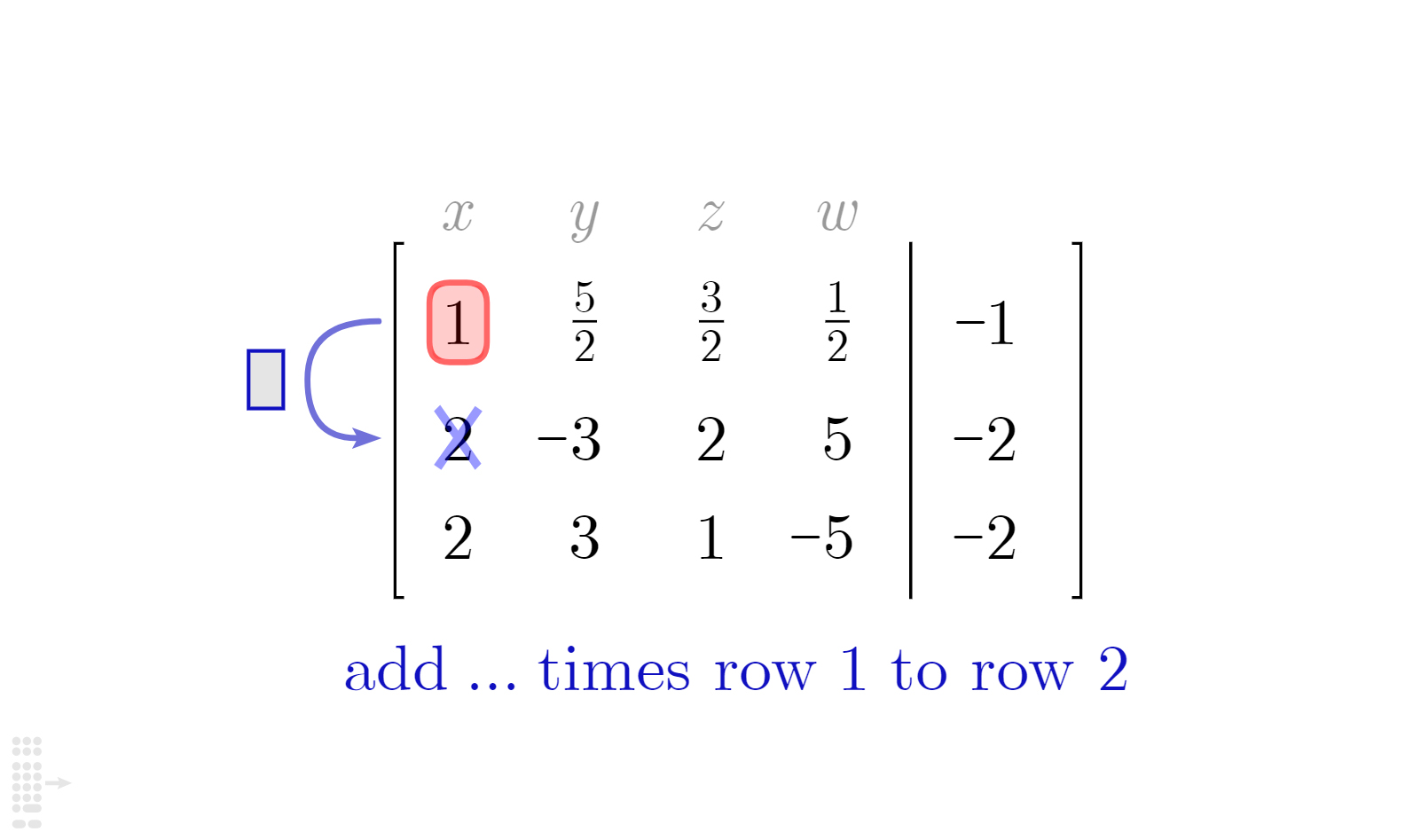
Solve system of linear equations using linsolve. Solving systems of linear equations using matrices. A linear equation is an equation for a straight line.

When x increases, y increases twice as fast, so we need 2x. Consider a linear system of equations with infinite solutions. A system of linear equations.

Y = 2x + 1. In this section, we will study linear systems consisting of two linear equations each with two variables. Given two matrices a and b, does there exist a unique matrix x, so that ax = b or xa = b?

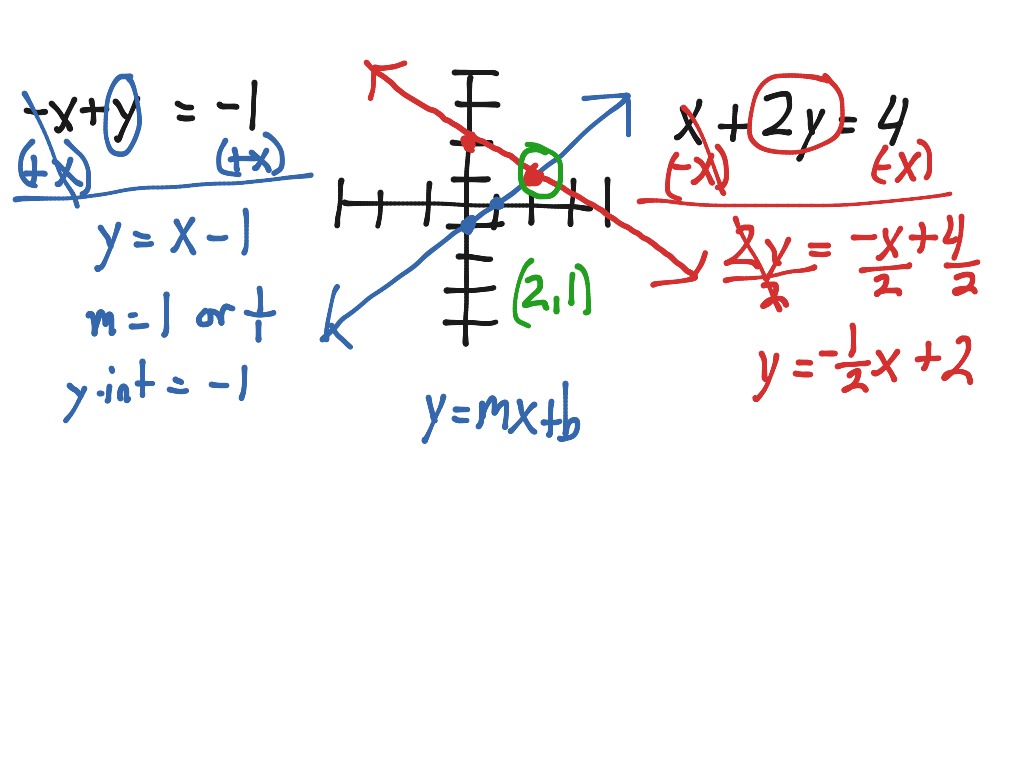
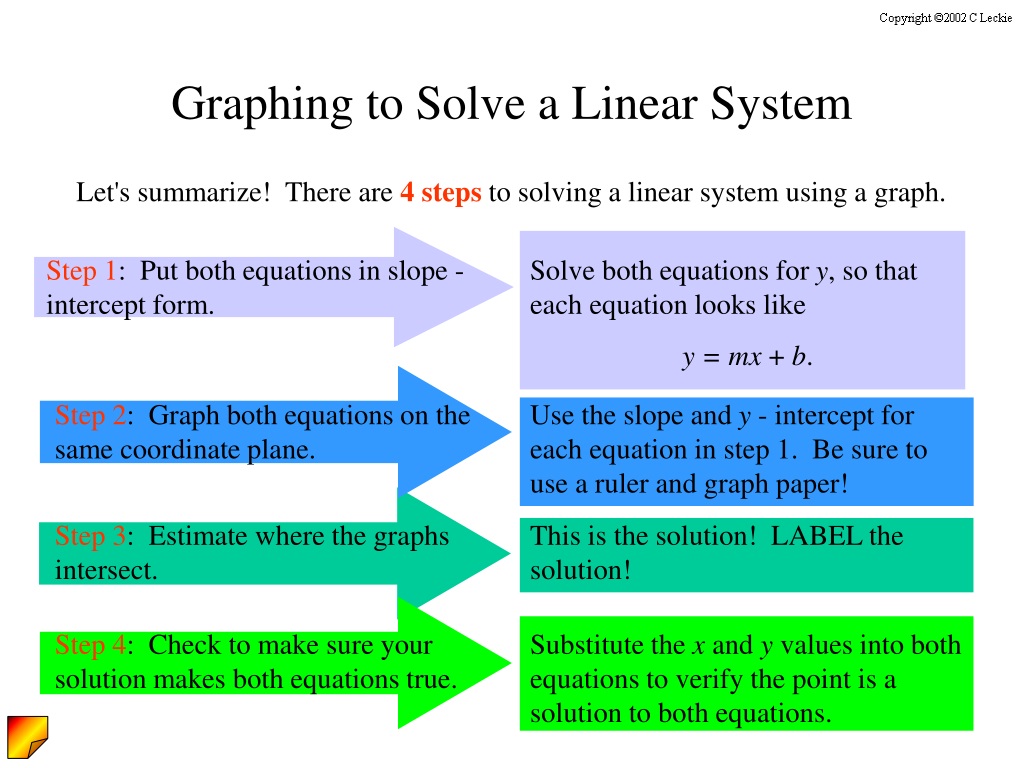
Make both equations into y = format. This means that there is one point that can satisfy all of the equations at the same time. A 1 n ⋮ ⋱ ⋮ a m 1 ⋯ a m n)

Systems of equations with graphing: + a 2 n x n = b 2 ⋯ a m 1 x 1 + a m 2 x 2 +. The easiest way to find a particular solution is to pick values for the free variables which then determines the values of the dependent variables.

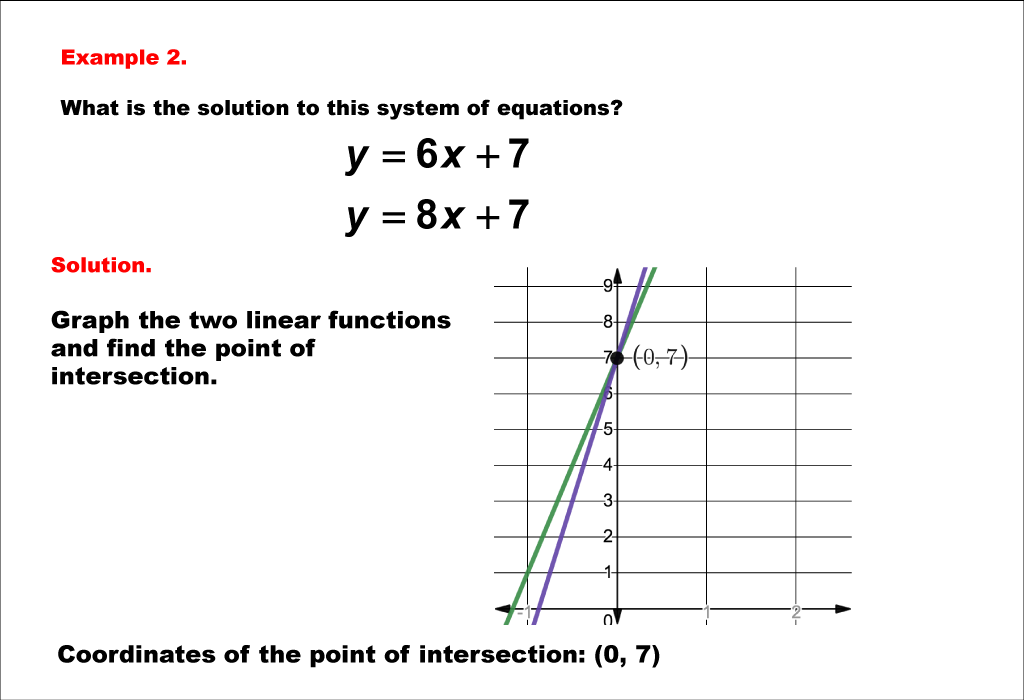
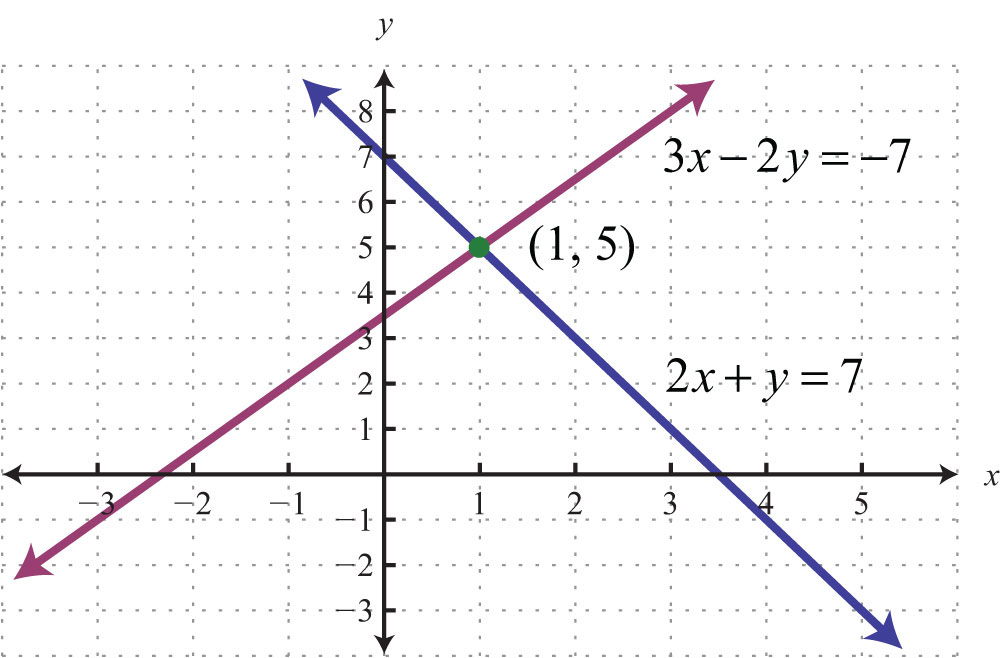
Now, pick your three (linearly independent) favourite vectors in $\mathbb{r}^3$, put in the places of $a_1, a_2, a_3$, compute the resulting $b$ and you have another system of linear equations with solution $x=1, y=2$, and $z=3$. Graphically (by plotting them both on the function grapher and zooming in) or using algebra. The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently.

Linear systems are a fundamental part of linear algebra, a subject used in most modern mathematics. Plug in all of your known values and use letters like x and y to represent the unknown variables. In the example above, a solution is given by the ordered triple since it makes all three equations valid.

Practice writing a system of linear equations that fits the constraints in a word problem. + a m n x n = b m. In other words, we are looking for the ordered pairs ( x , y ) that make both equations true.