Out Of This World Info About Does Curvature Mean Slope R Squared Excel Graph

What type of data is needed to create a slope or aspect layer?

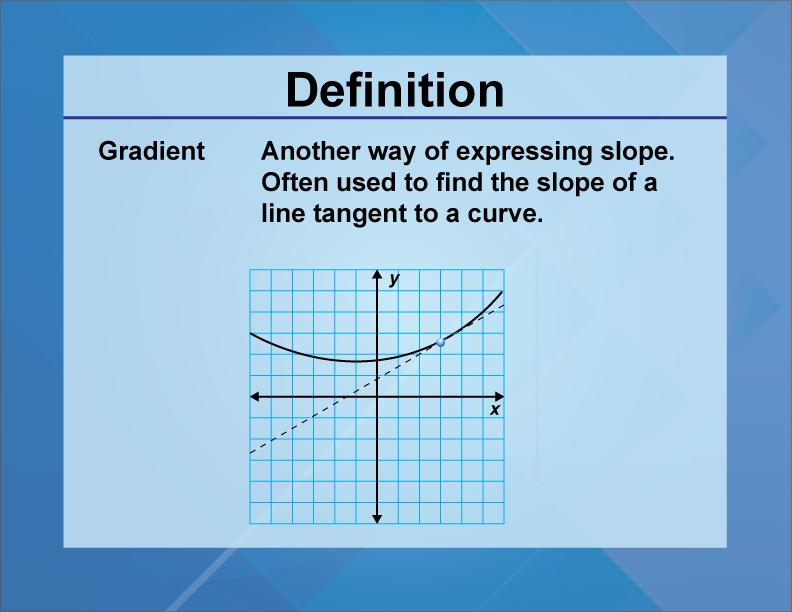
Does curvature mean slope. The curvature function displays the shape or curvature of the slope. The slope of a curve $\gamma$ at a point $p \in \gamma$ equals the slope of the line $l$ through $p$ that is a best fit for the curve to first order, which means: What does the output value within a cell mean after the aspect tool has been used?

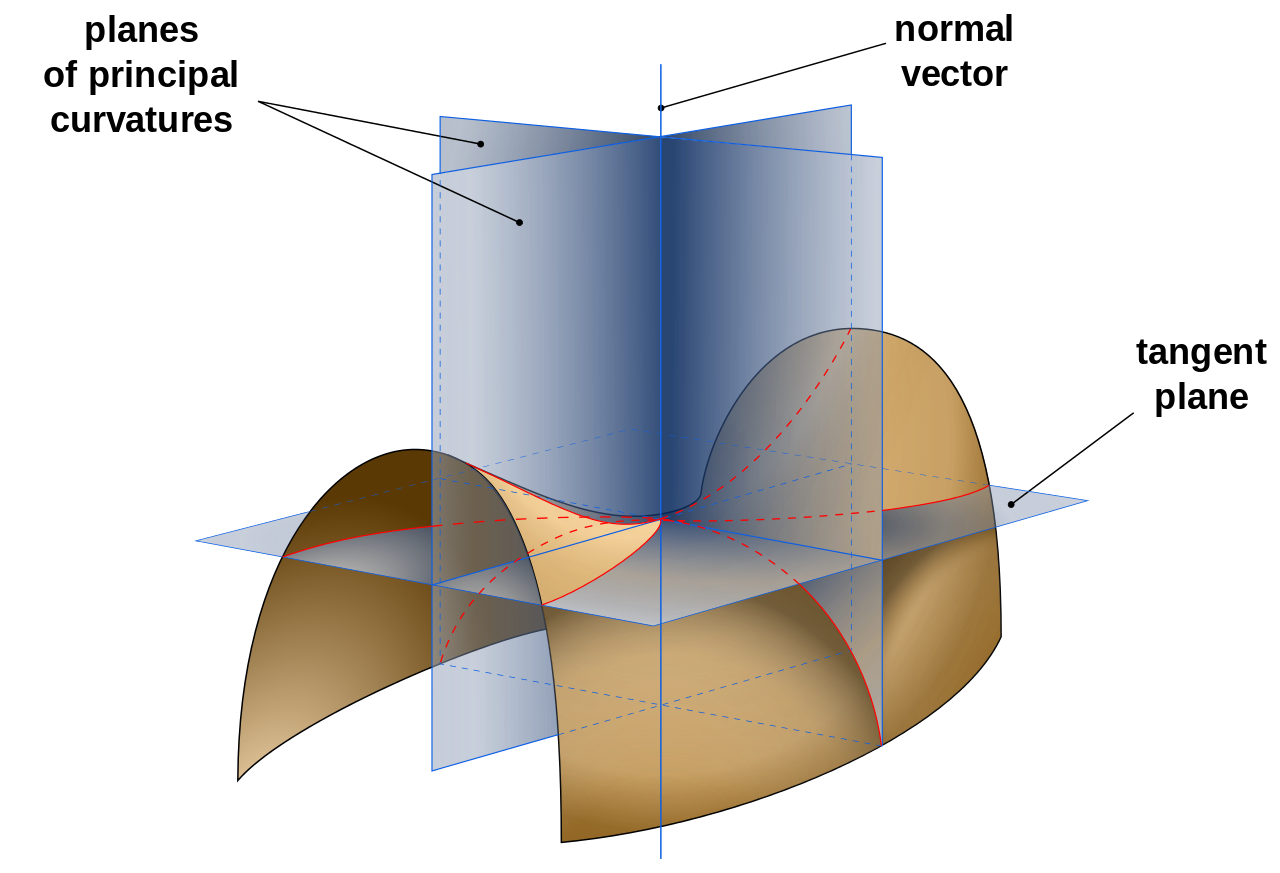
In order to see this curvature we will embed these objects in a space with one extra dimension. In most cases it is denoted by letter m. Curvature varies inversely under similarity:

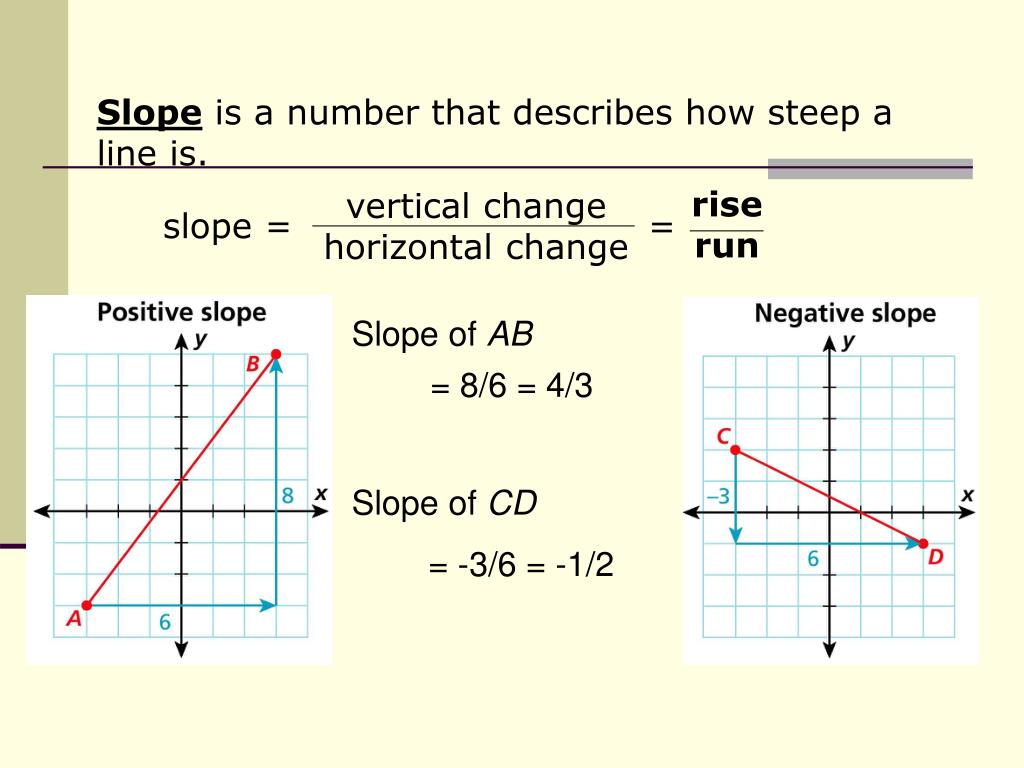
Is small, the signed curvature is well approximated by the second derivative. Often denoted by the letter m, slope is calculated as the ratio of the vertical change to the horizontal change (rise over run) between two distinct points on the line, giving the same number for any choice of points. The circle which best approximates a given curve near a given point is called the circle of curvature or the osculating circle 2 at the point.

It has a dimension of length −1. If a line goes up 2 steps for. Affects hydrological processes because of evapotranspiration [34] and then, influences soil moisture and vegetation cover [35,36].

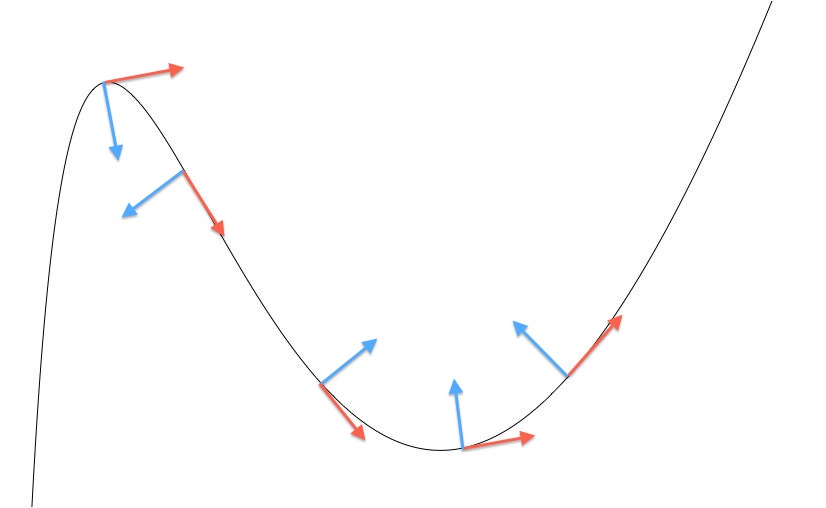
A part of a surface can be concave or convex; The curvature, denoted κ ‍ , is one divided by the radius of curvature. If the object is moving with a velocity of +4 m/s, then the slope of the line will be +4 m/s.

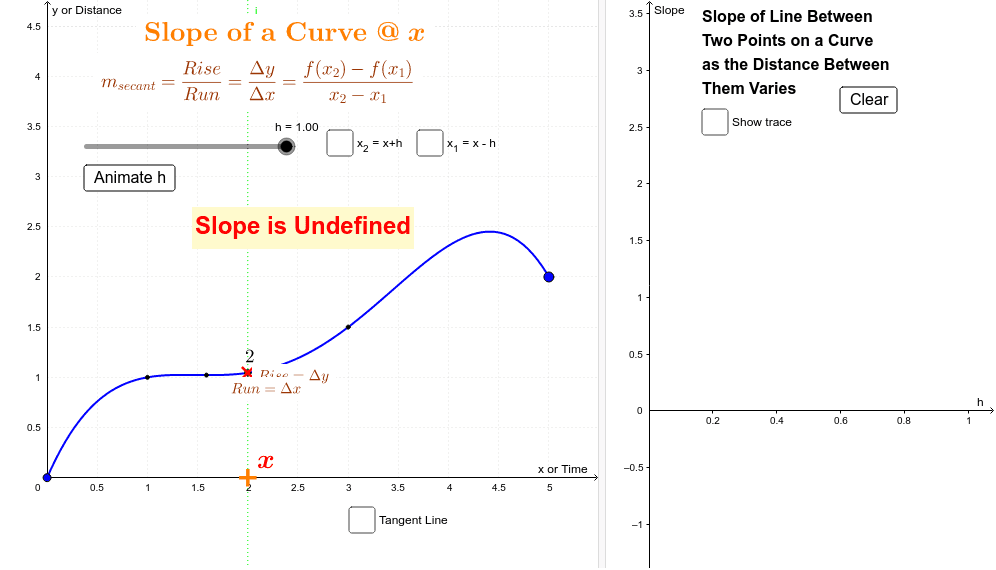
We find the slope by seeing how much we go up or down (vertical change) for each step to the right (horizontal change). Because tangent lines at certain point of a curve are defined as lines that barely touch the curve at the given point, we can deduce that tangent lines or vectors have slopes equivalent to the instantaneous slope of a curve at the given point. If slope is positive then the line is increasing,.

The curvature, on the other hand, is the inverse of the radius of the circle that best approximates the curve at that point, a.k.a. In mathematics, slope is a number that describes steepness and direction of a line. What does a greater curvature value tell you about a given surface?

Suppose $c$ and $c'$ are two curves such that $c$ is similar to $c'$. The curvature is calculated by computing the second derivative of the surface. The information about the slope aspect was.

In mathematics, the mean curvature of a surface is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as euclidean space. More precisely, using big o notation, one has. The slope of the curve at a point is equal to the slope of the line that best approximates the curve at that point, a.k.a.

This concept can also influence appraisal of the importance of various kinds of plan and profile curvature. In particular, a minimal surface such as a soap film has mean curvature zero and a soap bubble has If the given curve is \ (y=f (x),\) we evaluate \ (\dfrac { dy } { dx } \) or \ (f' (x)\) and substitute the value of \ (x\) to find the slope.